百叶轮抛光TC4温度仿真与试验

王丽博; 鲜超; 辛红敏

doi:10.13394/j.cnki.jgszz.2024.0019

百叶轮抛光TC4温度仿真与试验

doi: 10.13394/j.cnki.jgszz.2024.0019

王丽博^1, ,,
鲜超^2,,
辛红敏^2,

1.
河南机电职业学院智慧城市学院, 郑州 451192
2.
西北工业大学机电学院, 西安 710072

基金项目: 国家科技重大专项资助项目（2015ZX04001003）；国家自然科学基金面上项目（51675439）。

详细信息

作者简介:
鲜超，男，1987年生，博士、讲师、硕士研究生导师。主要研究方向：整体叶盘加工技术。E-mail：xianchao1994@163.com

辛红敏，女，1979年生，博士、教授、硕士研究生导师。主要研究方向：航空航天复杂结构件数控智能制造装备及工艺、冷喷涂增材制造、抗疲劳制造技术、物联网与智能交通技术。 E-mail：xhm0330@163.com

通讯作者:
王丽博，女，1984年生，硕士。主要研究方向：机械加工、控制技术。 E-mail：22995305@qq.com

中图分类号: TG580.14;V232.4
计量
- 文章访问数: 492
- HTML全文浏览量: 259
- PDF下载量: 2
- 被引次数: 0
出版历程
- 收稿日期: 2024-01-25
- 修回日期: 2024-04-29
- 录用日期: 2024-05-24
- 网络出版日期: 2024-05-24
- 刊出日期: 2025-06-30

Temperature simulation and experimental for polishing TC4 with abrasive cloth wheel

WANG Libo^{1
, ,},
XIAN Chao^2
,,
XIN Hongmin^2
,

1.
Smart City College, Henan Mechanical and Electrical Vocational College, Zhengzhou 451192, China
2.
School of Mechanical Engineering, Northwestern Polytechnical University, Xi'an 710072, China

摘要

摘要: 抛光温度是影响零件表面性能的重要因素，尤其会对零件表面残余应力的形成产生关键影响。通过试验测量百叶轮抛光TC4试件的抛光温度，基于矩形移动热源模型建立抛光温度的理论计算模型，并通过ANSYS仿真抛光TC4的表面温度。结果表明：抛光温度随主轴转速、百叶轮压缩量的增大而升高，随进给速度、磨粒目数的增大而降低。柔性抛光温度要显著低于刚性抛光温度，4个工艺参数中百叶轮压缩量的主效应最大，对抛光温度的影响程度最大。抛光温度梯度以正在加工的接触区域向已加工区域逐渐递减，抛光热效应对未加工区域影响较小。通过对比抛光温度测量结果、计算结果和仿真结果，发现仿真值和测量值的偏差率均 < 22%，计算值和测量值的偏差率均 < 17%。
- 百叶轮 /
- 抛光温度 /
- 理论模型
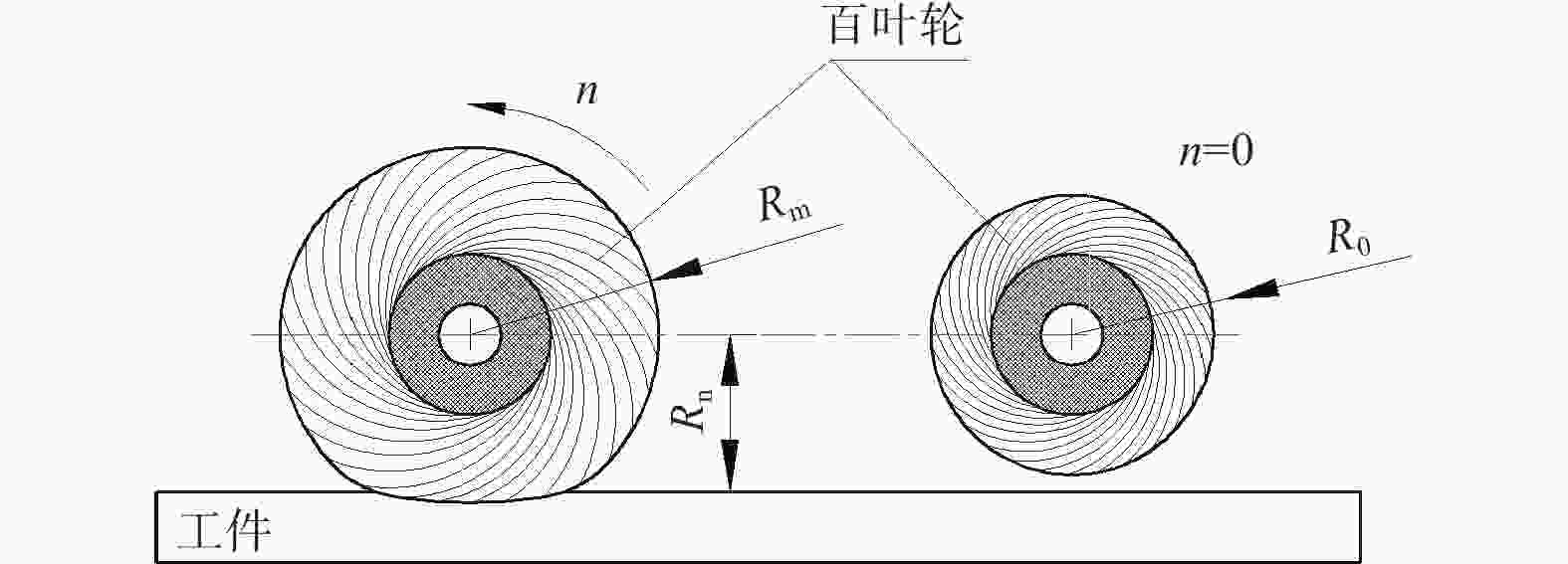
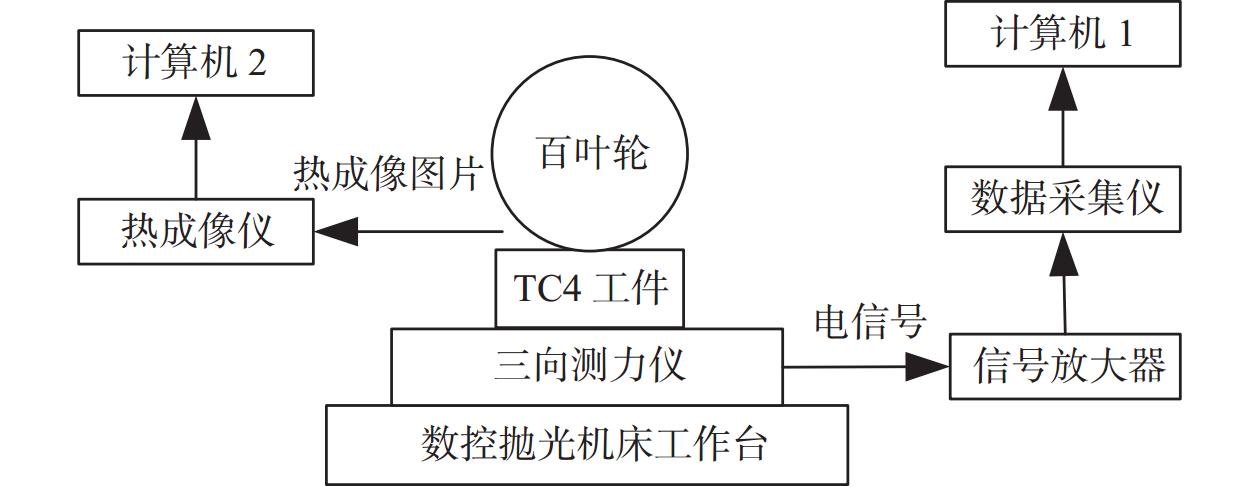
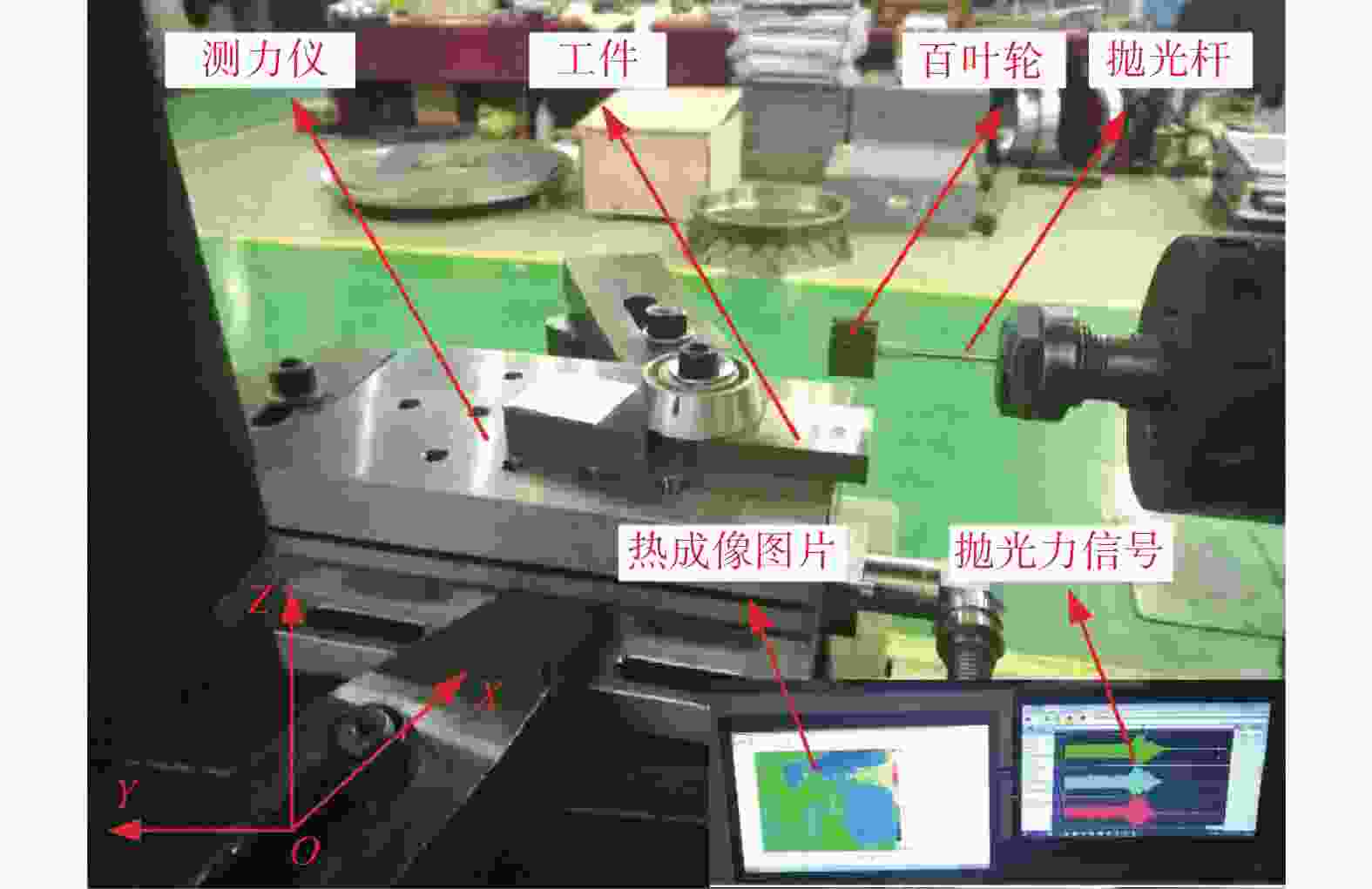
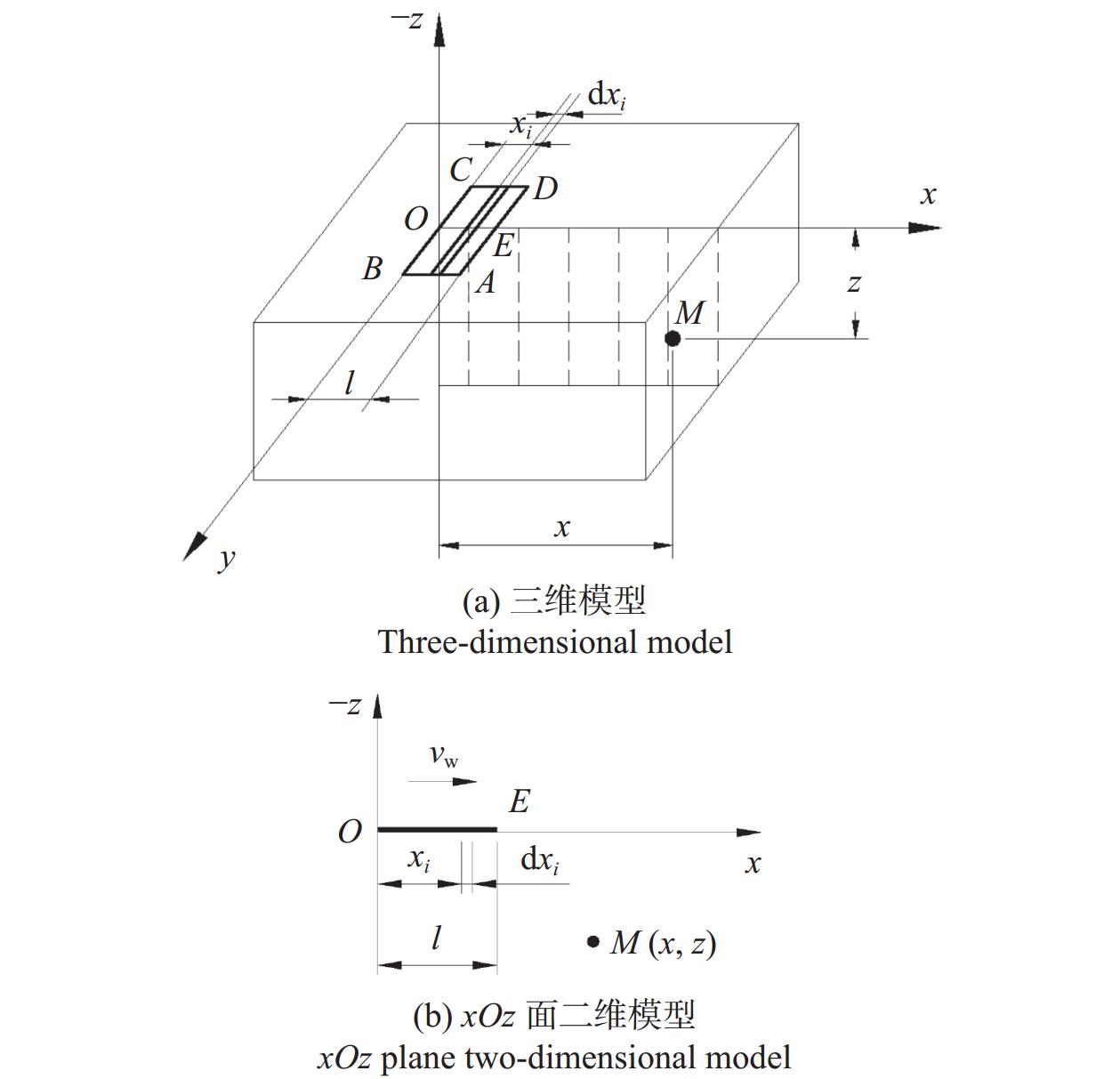
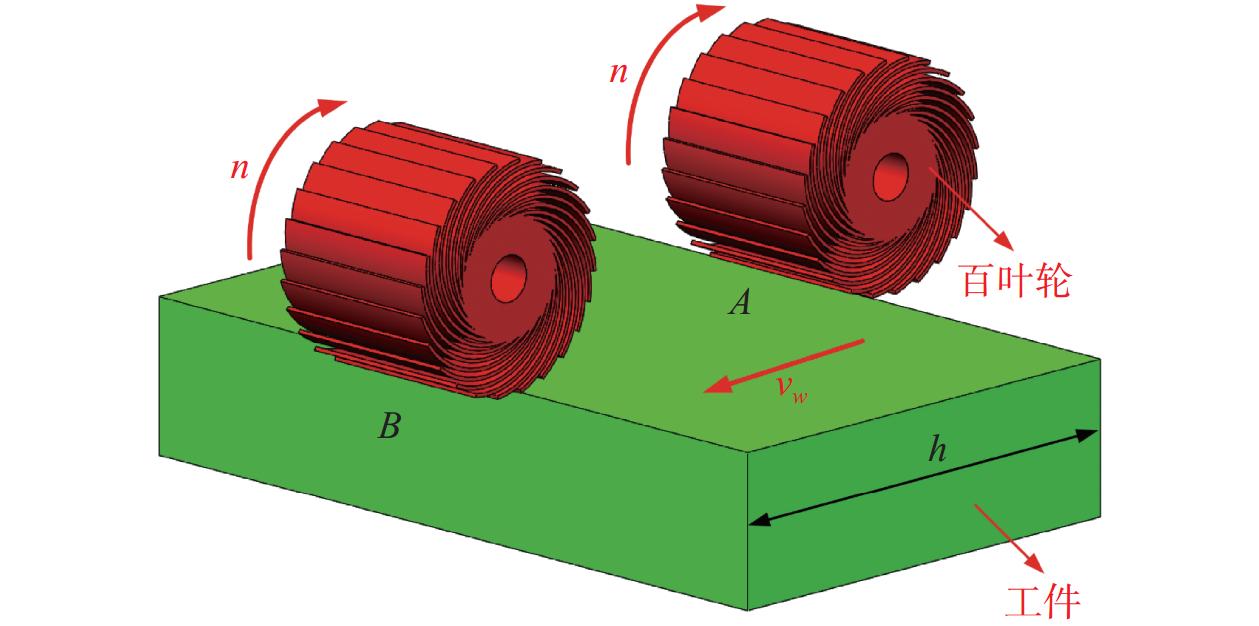
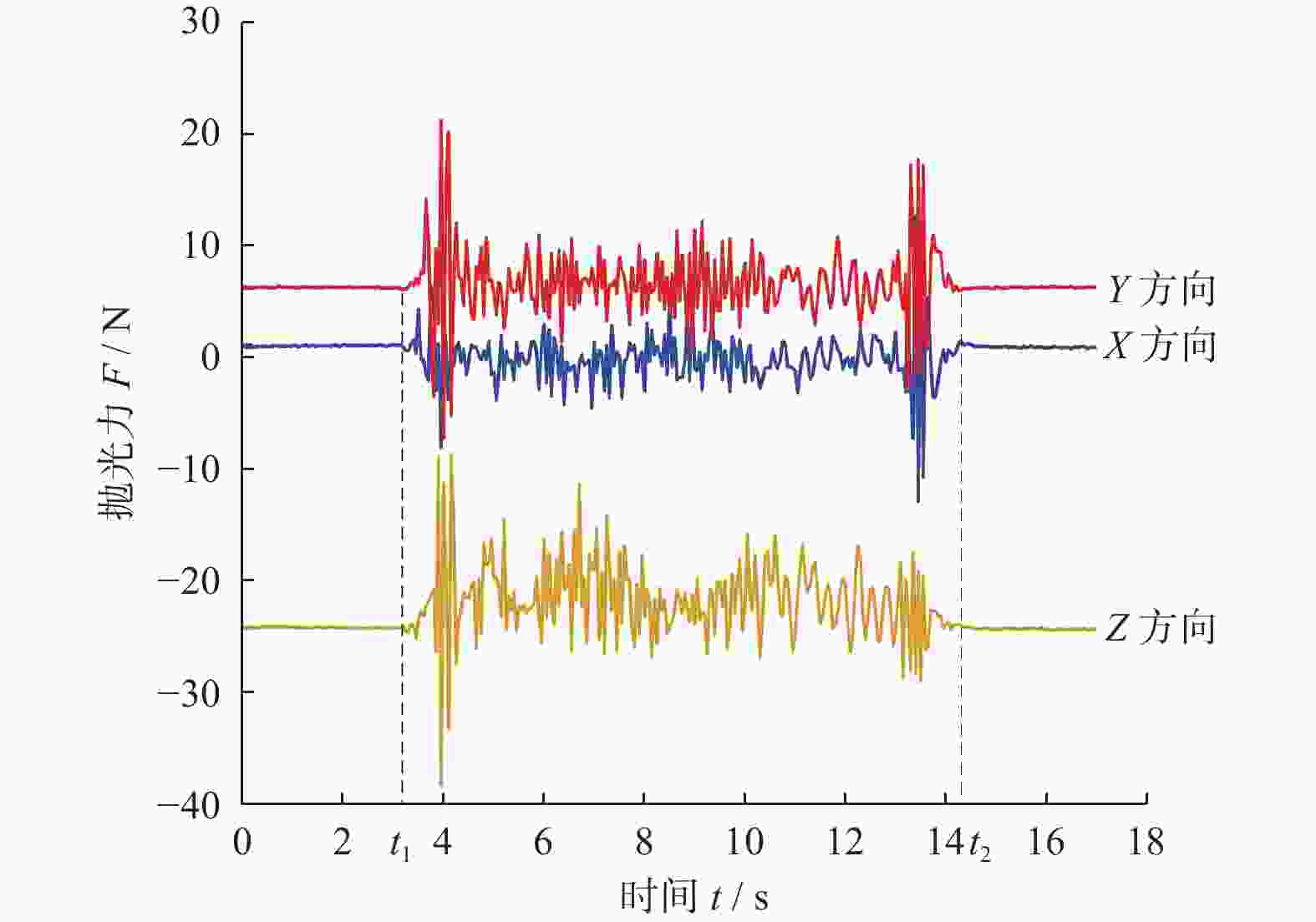
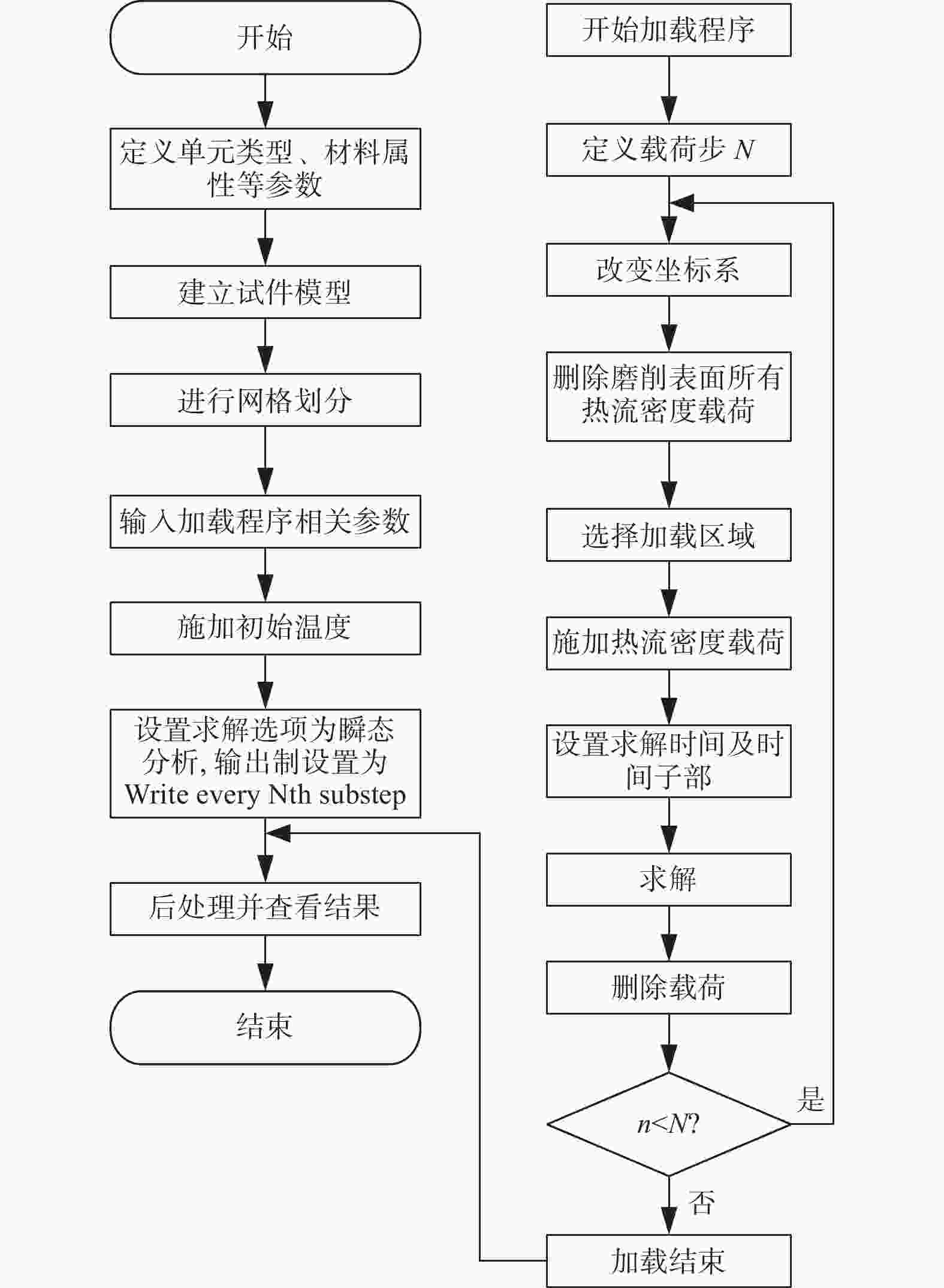
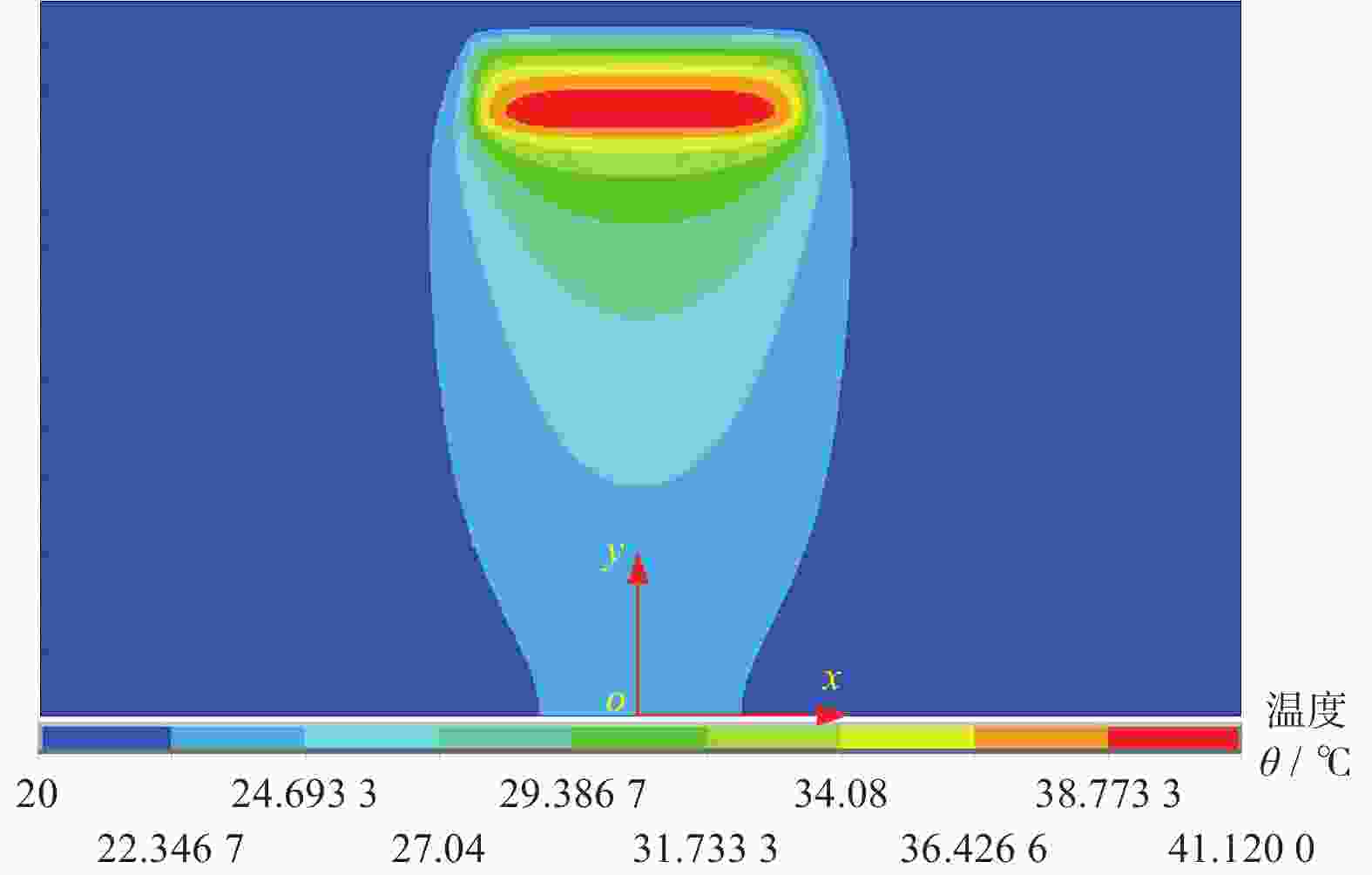
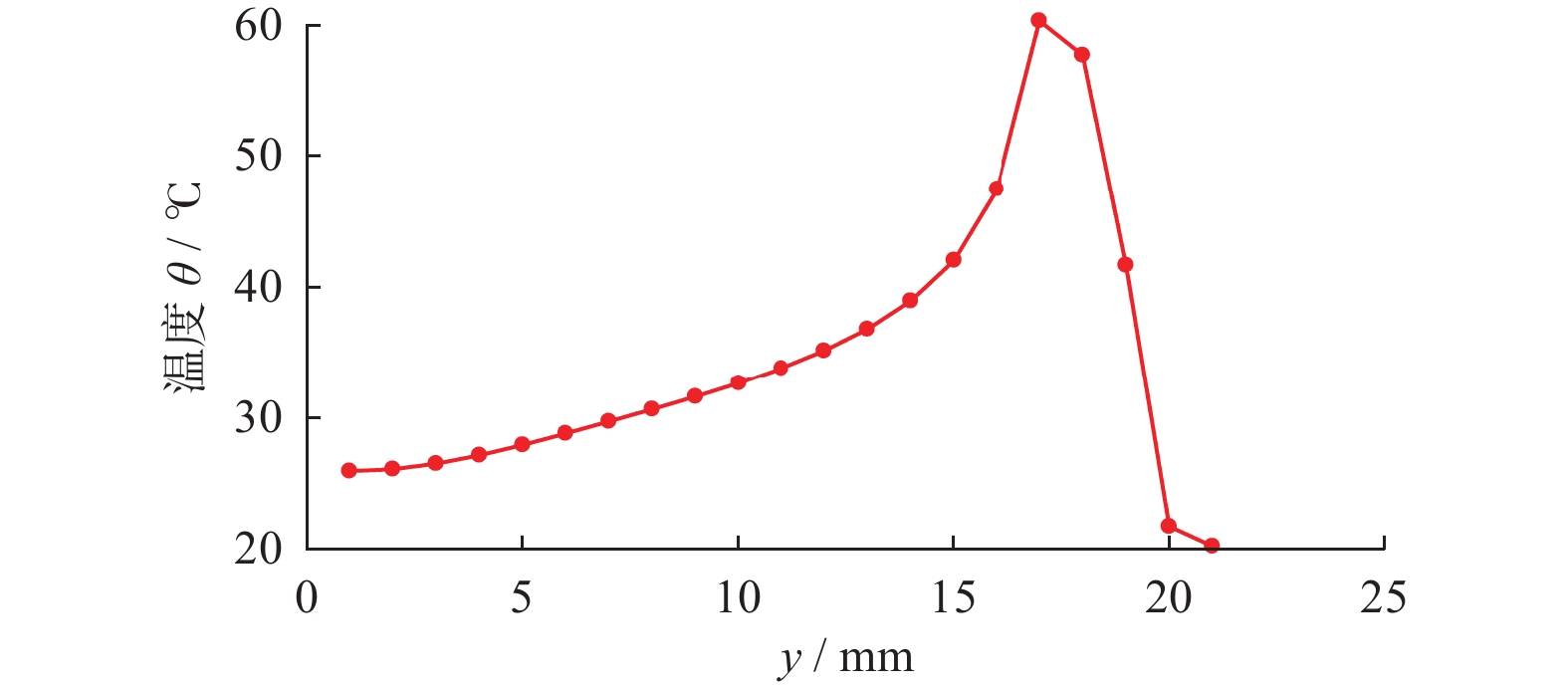
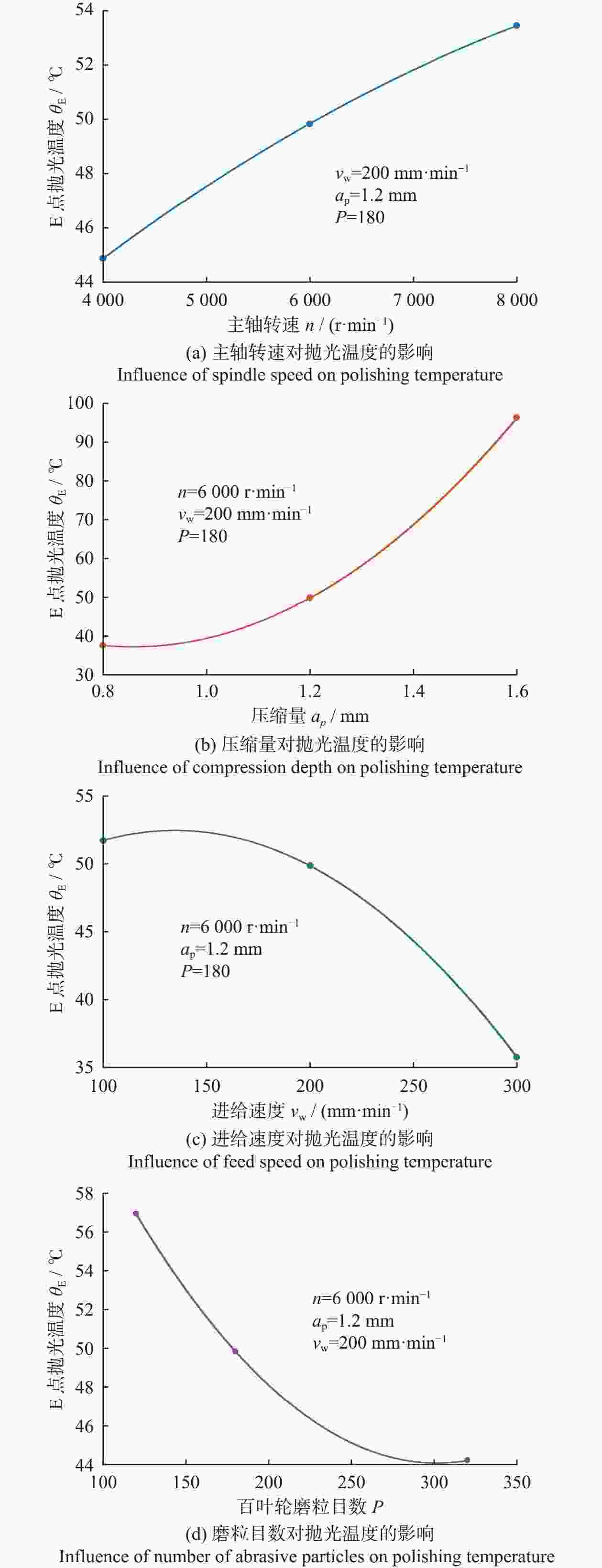
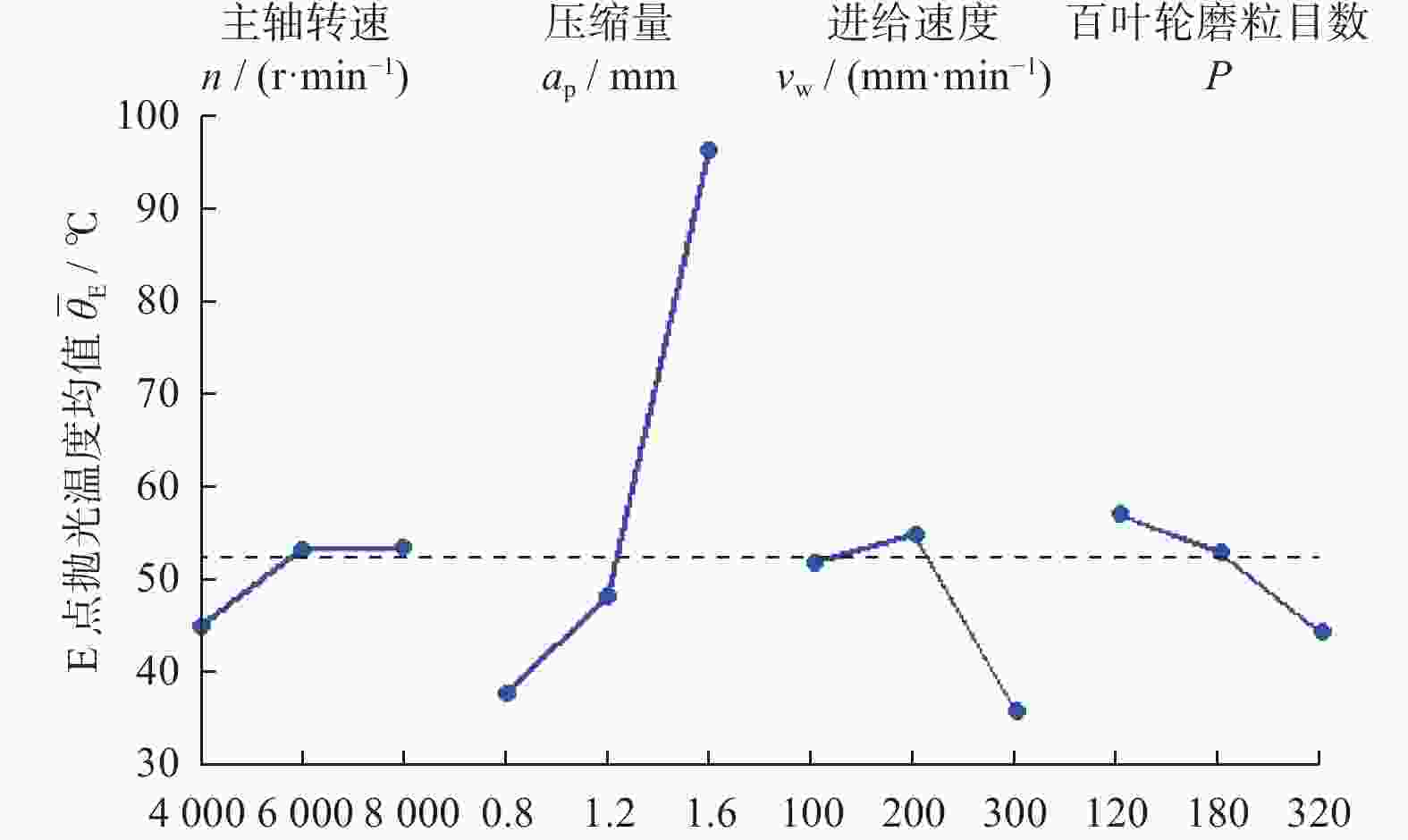
Abstract: Objectives During the polishing and grinding process, a large amount of heat is generated in the contact area between the grinding tool and the workpiece, while the amount of material removed is very small. Most of the heat is transferred to the workpiece, causing a rapid increase in temperature near the surface of the workpiece. This results in adverse effects such as residual tensile stress, white layer, and deformation, which negatively impact the surface quality and performance of parts. Therefore, studying the distribution laws and influencing factors of surface temperature in polishing and grinding, and controlling the processing surface temperature are of great significance. Methods A polishing test platform is built, and polishing temperatures are measured under different process parameters. The measured temperature values are corrected to obtain the actual temperature values. A theoretical model of the temperature field in the polishing contact area is derived based on the rectangular moving heat source model, and a temperature calculation model corresponding to the experimental measurement point is obtained, with the temperature value of that point calculated. The workpiece temperature field distribution during polishing is obtained using ANSYS simulation software and APDL for cyclic loading. The distribution law of the workpiece temperature field is studied, and the internal mechanism of this distribution law is explored. The temperature values corresponding to the experimental measurement points are extracted. The measured, calculated, and simulated values of temperature near the same point in the polishing contact area are compared. Based on the experimental results, single factor influence law figures of four process parameters on polishing temperature are drawn, and the influence mechanisms of the four process parameters on polishing temperature are explored. Based on the relationship between the radius increment and compression depth of abrasive cloth wheel, flexible polishing and rigid polishing are defined, and the effects of flexible and rigid polishing on polishing temperature are explored. A main effect analysis of process parameters is conducted with polishing temperature as the response and process parameters as the factors, to study the degree of influence of each process parameter on polishing temperature. Results Comparing the measurement results, calculation results, and simulation results of polishing temperature, it is found that the deviation rates between the simulation values and the measurement values are less than 22%, and the devia-tion rates between the calculated values and the measurement values are less than 17%. The deviations between simu-lated values and measured values are mainly due to the actual heat source model being complex, while the simulated heat source model uses a simplified rectangular heat source model, as well as measurement errors. The deviations between calculated and measured values are mainly caused by measurement errors in contact arc length, temperature, heat distribution coefficient, and the heat source model. The influence of four process parameters on polishing temperature is as follows: polishing temperature increases with the increase of spindle speed, because higher spindle speed results in greater linear velocity of the abrasive cloth wheel, and more work is done by the frictional force between the abrasive particles, binder, and workpiece per unit time, generating more heat and resulting in higher polishing temperature; polishing temperature increases with the increase of the compression depth of the abrasive cloth wheel. This is because larger compression depth leads to greater tangential force on a single abrasive particle, and more abrasive particles participate in cutting. More work is done by the frictional force between the abrasive particles, binder, and workpiece per unit time, generating more heat, and resulting in higher polishing temperature; polishing temperature decreases with the increase of feed rate. Although higher feed rate enhances heat source intensity, the contact time between the workpiece and the heat source is shorter, resulting in less heat transferred to the workpiece and lower polishing temperature; polishing temperature decreases with the increase of mesh number of abrasive particles. This is because a larger mesh number of abrasive particle means smaller abrasive particle size and more abrasive particles interacting with the workpiece in the contact area, making heat more easily carried away by the abrasive particles. At the same time, the larger the mesh number of abrasive particle, the smaller the abrasive particle size, the larger the contact area between the workpiece and grinding tool, the smaller the tangential force exerted on a single abrasive particle, and the less work done by frictional force between the abrasive particle and the workpiece per unit time, generating less heat. These two reasons together lead to a decrease in polishing temperature with the increase of mesh number of abrasive particles. A main effect analysis shows that compression depth has the largest main effect and the greatest influence on polishing temperature, while the other three process parameters have smaller main effects and less influence on polishing temperature. Conclusions The value of compression depth has the greatest influence on the polishing temperature and also affects whether the polishing state is rigid or flexible. Therefore, when determining the polishing process parameters, the appropriate compression depth should be selected first, and then other process parameters should be selected accordingly.
- abrasive cloth wheel /
- polishing temperature /
- theoretical model

HTML全文

图 1 百叶轮实物图

Figure 1. Physical picture of abrasive cloth wheels

下载: 全尺寸图片幻灯片

图 2 百叶轮柔性抛光原理

Figure 2. Principle of flexible polishing with abrasive cloth wheel

下载: 全尺寸图片幻灯片

图 3 抛光力和抛光温度测量原理

Figure 3. Principle of measuring polishing force and polishing temperature

下载: 全尺寸图片幻灯片

图 4 现场试验图

Figure 4. Field test

下载: 全尺寸图片幻灯片

图 5 热成像图片

Figure 5. Thermal image

下载: 全尺寸图片幻灯片

图 6 矩形热源移动模型

Figure 6. Moving rectangular heat source model

下载: 全尺寸图片幻灯片

图 7 抛光过程

Figure 7. Polishing process

下载: 全尺寸图片幻灯片

图 8 抛光力信号

Figure 8. Polishing force signal

下载: 全尺寸图片幻灯片

图 9 抛光温度仿真流程

Figure 9. Polishing temperature simulation process

下载: 全尺寸图片幻灯片

图 10 ANSYS仿真的磨削表面温度场

Figure 10. Simulated results of grinding surface temperature field by ANSYS

下载: 全尺寸图片幻灯片

图 11 表面温度随位置变化曲线

Figure 11. Variation curve of surface temperature with position

下载: 全尺寸图片幻灯片

图 12 温度的计算值、仿真值和测量值对比

Figure 12. Comparison for calculated, simulated, and measured values of temperature

下载: 全尺寸图片幻灯片

图 13 工艺参数对抛光温度的影响规律

Figure 13. Influence law of process parameters on polishing temperature

下载: 全尺寸图片幻灯片

图 14 主效应分析

Figure 14. Main effect analysis

下载: 全尺寸图片幻灯片

表 1 特殊函数i(p,ξ)的值

Table 1. Values of special function i(p,ξ)

p	i(p,1)(p < 0)	p	i(p,1)(p > 0)
−0.05	0.199	0.05	0.189
−0.10	0.343	0.10	0.300
−0.20	0.576	0.20	0.472
−0.30	0.777	0.30	0.595
−0.40	0.955	0.40	0.683
−0.50	1.113	0.50	0.748
−0.60	1.252	0.60	0.749
−0.70	1.381	0.80	0.857
−0.80	1.504	1.00	0.896
−0.90	1.624	1.20	0.914
−1.00	1.739	1.40	0.932
−1.20	1.957	1.60	0.944
−1.40	2.160	1.80	0.947
−1.60	2.347	2.00	0.955
−1.80	2.528	2.20	0.958
−2.00	2.703	2.40	0.960
−2.20	2.871	2.60	0.961
−2.40	3.032	2.80	0.962
−2.60	3.188	3.00	0.962
−2.80	3.337	3.50	0.963
−3.00	3.481	4.00	0.963
−3.50	3.824	4.50	0.963
−4.00	4.154	5.00	0.963
−4.50	4.446	6.00	0.963
−5.00	4.749	7.00	0.963
−5.50	5.025	8.00	0.963
−6.00	5.290	9.00	0.963
−7.00	5.772
−8.00	6.231
−9.00	6.661
−10.0	7.068
−12.0	7.825
−14.0	8.523
−16.0	9.171
−18.0	9.780
−20.0	10.350
−22.0	10.910

下载: 导出CSV

表 2 不同目数百叶轮对应的筛孔直径

Table 2. Sieve diameters corresponding to abrasive cloth wheels with different number of abrasive particles

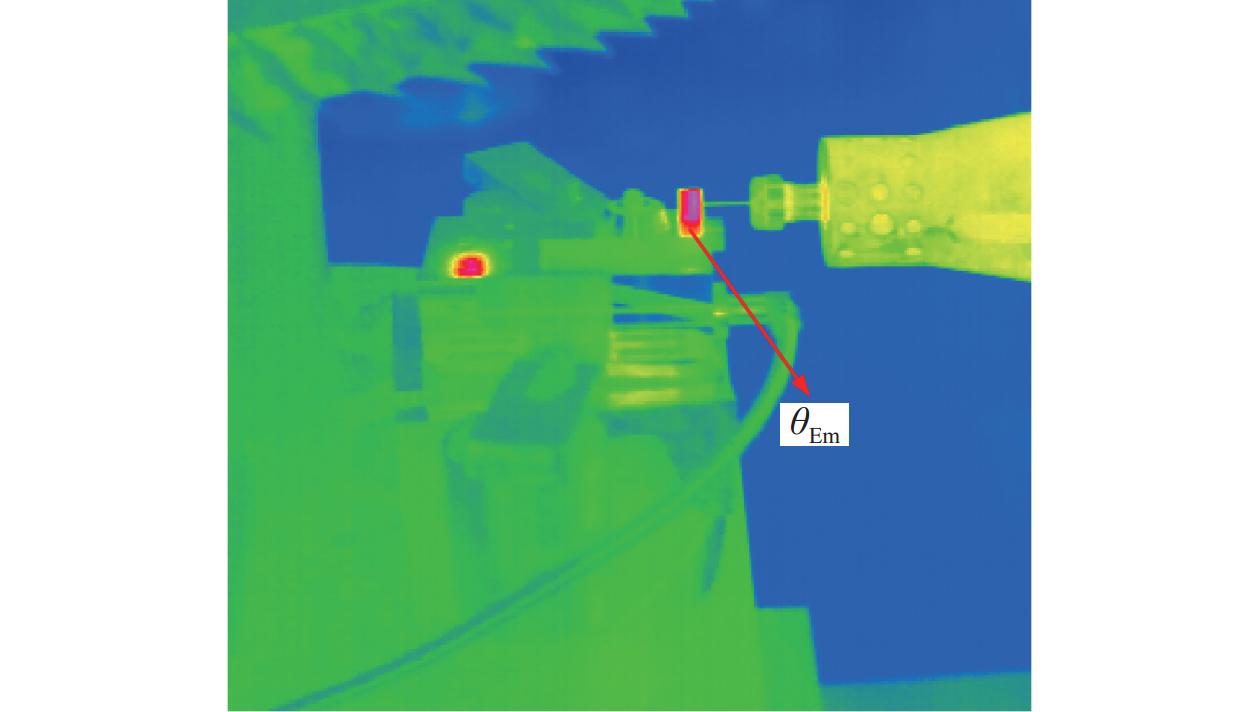
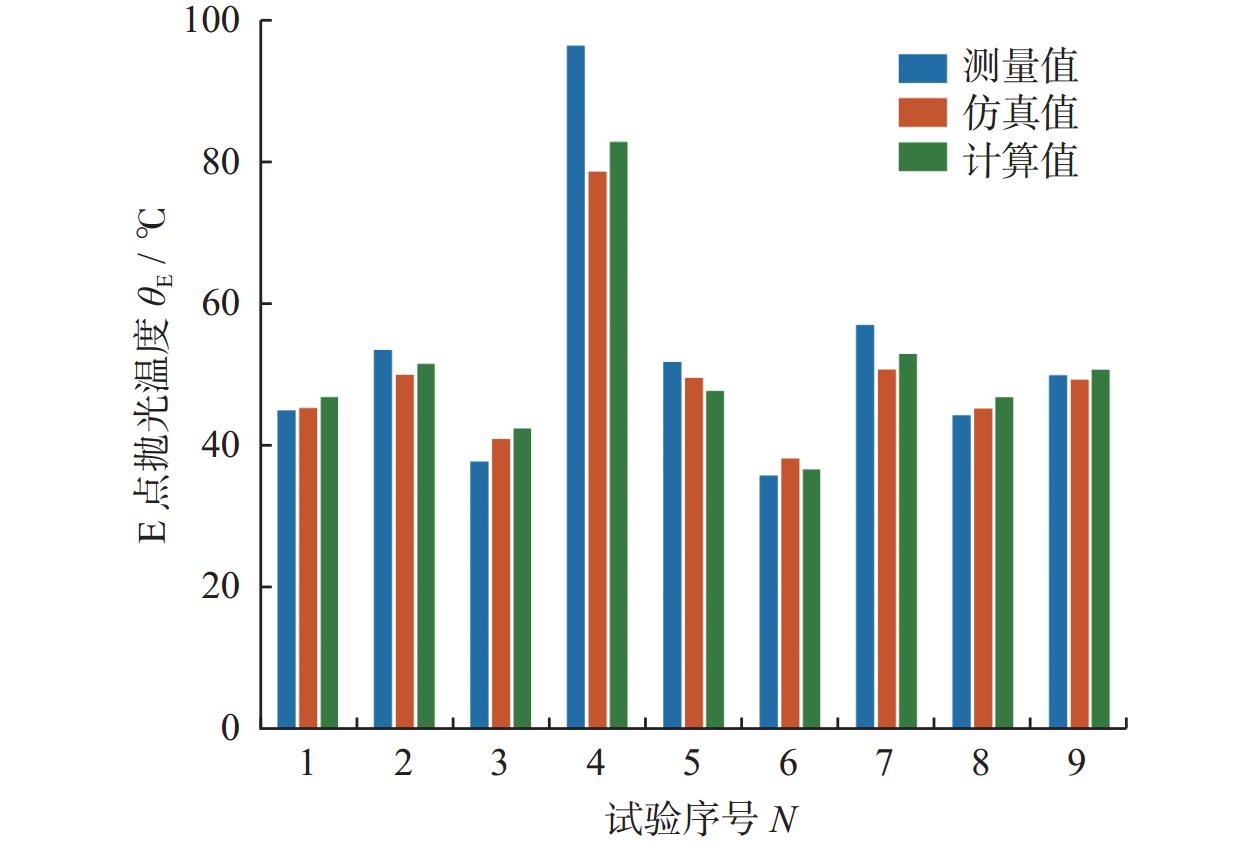
百叶轮目数 P	筛孔直径 d / μm
240	61
320	44
400	38
600	23
1 000	13

下载: 导出CSV

表 3 TC4在20 ℃时物理性能参数^[38]

Table 3. Physical performance parameters of TC4 at 20 ℃^[38]

性能参数	数值
密度 ρ / (kg·m⁻³)	4 450
比热容 c / (J·kg⁻¹·℃⁻¹)	612
热导率 λ / (W·m⁻¹·K⁻¹)	5.44

下载: 导出CSV

表 4 E点温度的计算值、仿真值和测量值结果

Table 4. Calculation, simulation, and measurement results of temperature at point E

序号	主轴转速 n / (r·min⁻¹)	百叶轮压缩量 a_p / mm	进给速度 v_w / (mm·min⁻¹)	百叶轮磨粒目数 P	抛光力 F_t / N	测量值 θ_Em / ℃	仿真值 θ_Es / ℃	计算值 θ_Ec / ℃
1	4 000	1.2	200	180	6.38	44.87	45.22	46.76
2	8 000	1.2	200	180	11.78	53.45	49.96	51.48
3	6 000	0.8	200	180	1.90	37.66	40.89	42.39
4	6 000	1.6	200	180	55.39	96.36	78.55	82.78
5	6 000	1.2	100	180	7.27	51.71	49.47	47.67
6	6 000	1.2	300	180	12.46	35.72	38.12	36.55
7	6 000	1.2	200	120	30.55	56.95	50.64	52.83
8	6 000	1.2	200	320	8.83	44.22	45.15	46.74
9	6 000	1.2	200	180	9.46	49.85	49.25	50.61

下载: 导出CSV

参考文献(38)

[1]	JAEGER J C. Moving sources of heat and the temperature at sliding contacts [J]. Journal and Proceedings of the Royal Society of New South Wales,1943,76(3):203-224. doi: 10.5962/p.360338
[2]	贝季瑶. 磨削温度的分析与研究 [J]. 上海交通大学学报,1964(3):55-71. doi: 10.16183/j.cnki.jsjtu.1964.03.005 BEI Jiyao. Analysis and research on grinding temperature [J]. Journal of Shanghai Jiao Tong University,1964(3):55-71. doi: 10.16183/j.cnki.jsjtu.1964.03.005
[3]	张磊. 单程平面磨削淬硬技术的理论分析和试验研究 [D]. 济南: 山东大学, 2006. ZHANG Lei. Theoretical analysis and experimental study on hardening technology of single-pass plane grinding [D]. Jinan: Shandong University, 2006.
[4]	金滩. 高效深切磨削技术的基础研究[D]. 沈阳: 东北大学, 1999. JIN Tan. Fundamental research on high efficiency deep grinding technology [D]. Shenyang: Northeastern University, 1999.
[5]	JIN T, CAI G Q. Analytical thermal models of oblique moving heat source for deep grinding and cutting [J]. Journal of Manufacturing Science and Engineering,2001,123(2):185-190. doi: 10.1115/1.1343458
[6]	JIN T, ROWE W B, MCCORMACK D. Temperatures in deep grinding of finite workpieces [J]. International Journal of Machine Tools and Manufacture,2002,42(1):53-59. doi: 10.1016/S0890-6955(01)00094-3
[7]	LIU M Z, LI C H, ZHANG Y B, et al. Analysis of grain tribology and improved grinding temperature model based on discrete heat source [J]. Tribology International,2023,180:108196. doi: 10.1016/j.triboint.2022.108196
[8]	YANG S Y, CHEN W F, NONG S, et al. Temperature field modelling in the form grinding of involute gear based on high-order function moving heat source [J]. Journal of Manufacturing Processes,2022,81:1028-1039. doi: 10.1016/j.jmapro.2022.07.014
[9]	GRIMMERT A, PACHNEK F, WIEDERKEHR P. Temperature modeling of creep-feed grinding processes for nickel-based superalloys with variable heat flux distribution [J]. CIRP Journal of Manufacturing Science and Technology,2023,41:477-489. doi: 10.1016/j.cirpj.2023.01.011
[10]	LAN S L, JIAO F. Modeling of heat source in grinding zone and numerical simulation for grinding temperature field [J]. The International Journal of Advanced Manufacturing Technology,2019,103(5):3077-3086. doi: 10.1007/s00170-019-03662-w
[11]	蒋培军. 基于温度匹配法的平面磨削3D有限元仿真及试验 [J]. 金刚石与磨料磨具工程,2020,40(5):96-101. doi: 10.13394/j.cnki.jgszz.2020.05.0017 JIANG Peijun. Three dimensional simulation and experiment of plane grinding temperature field based on temperature matching method [J]. Diamond & Abrasives Engineering,2020,40(5):96-101. doi: 10.13394/j.cnki.jgszz.2020.05.0017
[12]	张宇. cBN砂轮对GCr15钢的磨削硬化试验与仿真研究[D]. 太原: 太原理工大学, 2020. ZHANG Yu. The experimental study and simulation ongrind-hardening of GCr15 steel by cBN grinding wheel [D]. Taiyuan: Taiyuan University of Technology, 2020.
[13]	王长清, 郑子琦, 郑勇, 等. 磨粒形状对轴类零件磨削温度影响的仿真分析 [J]. 组合机床与自动化加工技术,2022(3):141-144. doi: 10.13462/j.cnki.mmtamt.2022.03.034 WANG Changqing, ZHENG Ziqi, ZHENG Yong, et al. Simulation analysis of influence of abrasive shape on grinding temperature of shaft part [J]. Modular Machine Tool & Automatic Manufacturing Technique,2022(3):141-144. doi: 10.13462/j.cnki.mmtamt.2022.03.034
[14]	孙为钊. 基于有限元和卷积神经网络的磨削温度理论分析及数值仿真 [D]. 上海: 上海工程技术大学, 2020. SUN Weizhao. Theoretical analysis and numerical simulation of grinding temperature based on finite element and convolutional neural network [D]. Shanghai: Shanghai University of Engineering Science, 2020.
[15]	YANG M, LI C H, ZHANG Y B, et al. Research on microscale skull grinding temperature field under different cooling conditions [J]. Applied Thermal Engineering,2017,126:525-537. doi: 10.1016/j.applthermaleng.2017.07.183
[16]	HANDA D, KUMAR S, SURENDRAN S B T, et al. Simulation of intermittent grinding for Ti-6Al-4V with segmented wheel [J]. Materials Today: Proceedings,2021,44:2537-2542. doi: 10.1016/j.matpr.2020.12.626
[17]	尹国强, 巩亚东, 李宥玮, 等. 新型点磨削砂轮磨削温度仿真实验 [J]. 东北大学学报(自然科学版),2019,40(3):392-397. doi: 10.12068/j.issn.1005-3026.2019.03.017 YIN Guoqiang, GONG Yadong, LI Youwei, et al. Simulation experiment of grinding temperature for novel point grinding wheel [J]. Journal of Northeastern University (Natural Science),2019,40(3):392-397. doi: 10.12068/j.issn.1005-3026.2019.03.017
[18]	李厦, 王锴霖. 超声振动辅助缓进给磨削温度场仿真与试验分析 [J]. 表面技术,2018,47(7):265-269. doi: 10.16490/j.cnki.issn.1001-3660.2018.07.040 LI Sha, WANG Kailin. Simulation and experimental analysis of ultrasonic vibration assisted creep feed grinding temperature field [J]. Surface Technology,2018,47(7):265-269. doi: 10.16490/j.cnki.issn.1001-3660.2018.07.040
[19]	朱贵升. 切向超声辅助磨削热力耦合特性研究[D]. 天津: 天津科技大学, 2022. ZHU Guisheng. Study on thermal-mechanical couplingcharaceristics of tangential ultrasonicssisted grinding [D]. Tianjin: Tianjin University of Science and Technology, 2022.
[20]	王晓旭. TC4钛合金纵扭超声磨削CBN砂轮磨损机理及其试验研究 [D]. 焦作: 河南理工大学, 2022. WANG Xiaoxu. Wear mechanism and experimental study of CBN grinding wheel in longitudinal and torsional ultrasonic grinding of TC4 titanium alloy [D]. Jiaozuo: Henan Polytechnic University, 2022.
[21]	BABBAR A, JAIN V, GUPTA D, et al. Finite element simulation and integration of CEM43 ℃ and Arrhenius models for ultrasonic-assisted skull bone grinding: A thermal dose model [J]. Medical Engineering & Physics,2021,90:9-22. doi: 10.1016/j.medengphy.2021.01.008
[22]	王晨晨. 骨骼磨削温度的仿真预测及实验研究 [D]. 青岛: 山东科技大学, 2021. WANG Chenchen. Research on the prediction based on simulation results and experimental of bone grinding temperature [D]. Qingdao: Shandong University of Science and Technology, 2021.
[23]	WAN L L, LI L, DENG Z H, et al. Thermal-mechanical coupling simulation and experimental research on the grinding of zirconia ceramics [J]. Journal of Manufacturing Processes,2019,47:41-51. doi: 10.1016/j.jmapro.2019.09.024
[24]	李征, 丁文锋, 周欢, 等. 基于混合材料模型的颗粒增强钛基复材高速磨削温度研究 [J]. 机械工程学报,2019,55(21):186-198. doi: 10.3901/JME.2019.21.186 LI Zheng, DING Wenfeng, ZHOU Huan, et al. Grinding temperature of particulate reinforced titanium matrix composites in high-speed grinding based on multi-material model [J]. Journal of Mechanical Engineering,2019,55(21):186-198. doi: 10.3901/JME.2019.21.186
[25]	刘军, 范宝朋, 陈燕, 等. 超声振动磨削CFRP温度场的有限元仿真 [J]. 机械科学与技术,2020,39(6):821-828. doi: 10.13433/j.cnki.1003-8728.20190217 LIU Jun, FAN Baopeng, CHEN Yan, et al. FEM simulation of temperature field in ultrasonic vibration grinding of CFRP [J]. Mechanical Science and Technology for Aerospace Engineering,2020,39(6):821-828. doi: 10.13433/j.cnki.1003-8728.20190217
[26]	SU J X, KE Q X, DENG X Z, et al. Numerical simulation and experimental analysis of temperature field of gear form grinding [J]. The International Journal of Advanced Manufacturing Technology,2018,97(5):2351-2367. doi: 10.1007/s00170-018-2079-6
[27]	GUO H, WANG X Y, ZHAO N, et al. Simulation analysis and experiment of instantaneous temperature field for grinding face gear with a grinding worm [J]. The International Journal of Advanced Manufacturing Technology,2022,120(7):4989-5001. doi: 10.1007/s00170-022-09036-z
[28]	GUO Z F, YI J, HU X P, et al. Heat flux distribution model and transient temperature field analysis in grinding of helical raceway [J]. The International Journal of Advanced Manufacturing Technology,2022,121(9):6497-6506. doi: 10.1007/s00170-022-09736-6
[29]	胡浩. 镍基高温合金螺纹成形磨削温度场仿真与实验研究[D]. 长沙: 湖南大学, 2022. HU Hao. Simulation and experimental study of temperature field in thread forming grinding of nickel-based superalloy [D]. Changsha: Hunan University, 2022.
[30]	KUANG W J, MIAO Q, DING W F, et al. Residual stresses of turbine blade root produced by creep-feed profile grinding: Three-dimensional simulation based on workpiece–grain interaction and experimental verification [J]. Journal of Manufacturing Processes,2021,62:67-79. doi: 10.1016/j.jmapro.2020.11.045
[31]	CHEN H, ZHAO J, DAI Y X, et al. Simulation of 3D grinding temperature field by using an improved finite difference method [J]. The International Journal of Advanced Manufacturing Technology,2020,108(11):3871-3884. doi: 10.1007/s00170-020-05513-5
[32]	王崇. 工程陶瓷高速磨削温度的有限元仿真分析 [D]. 长沙: 湖南大学, 2021. WANG Chong. Finite element simulation analysis of high-speed grinding temperature of engineering ceramics [D]. Changsha: Hunan University, 2021.
[33]	赵玲刚. 氮化硅陶瓷磨削温度与表面变质层的仿真与实验 [J]. 机械与电子,2021,39(10):9-14. doi: 10.3969/j.issn.1001-2257.2021.10.002 ZHAO Linggang. Simulation and experiment of grinding temperature and surface modification layer of silicon nitride ceramics [J]. Machinery & Electronics,2021,39(10):9-14. doi: 10.3969/j.issn.1001-2257.2021.10.002
[34]	陆子凤. 红外热像仪的辐射定标和测温误差分析[D]. 长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2010. LU Zifeng. Calibration and the measurement error analysis of infrared imaging system for temperature measurement [D]. Changchun: Graduate School of Chinese Academy of Sciences (Changchun Institute of Optical Precision Machinery and Physics), 2010.
[35]	任敬心, 华定安. 磨削原理 [M]. 北京: 电子工业出版社, 2011. REN Jingxin, HUA Dingan. Grinding principle [M]. Beijing: Publishing House of Electronics Industry, 2011.
[36]	ROWE W B, BLACK S C E, MILLS B, et al. Grinding temperatures and energy partitioning [J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences,1997,453(1960):1083-1104. doi: 10.1098/rspa.1997.0061
[37]	鲜超, 史耀耀, 蔺小军, 等. 百叶轮抛光TC4的接触弧长试验研究 [J]. 计算机集成制造系统,2020,26(5):1218-1232. doi: 10.13196/j.cims.2020.05.008 XIAN Chao, SHI Yaoyao, LIN Xiaojun, et al. Experimental study on contact arc length of polishing TC4 with abrasive cloth wheel [J]. Computer Integrated Manufacturing Systems,2020,26(5):1218-1232. doi: 10.13196/j.cims.2020.05.008
[38]	宝鸡旭隆有色金属有限公司. 钛合金TC4性能介绍[EB/OL]. (2022-12-07)[2024-04-18]. https://www.sxxlti.com/titanium-rods/194.html. Baoji Xulong Nonferrous Metals Co., Ltd. Introduction to the performance of titanium alloy TC4 [EB/OL]. (2022-12-07)[2024-04-18]. https://www.sxxlti.com/titanium-rods/194.html.