基于控制研磨深度的金刚石研磨质量分析

庞飞; 雷大江; 王伟

doi:10.13394/j.cnki.jgszz.2022.0048

基于控制研磨深度的金刚石研磨质量分析

doi: 10.13394/j.cnki.jgszz.2022.0048

庞飞^{1, 2,},
雷大江¹,
王伟²

1.
中国工程物理研究院机械制造工艺研究所, 四川绵阳 621000
2.
电子科技大学机械与电气工程学院, 成都 611731

基金项目: 国家科技重大专项（2017ZX04022001）

详细信息

作者简介:
庞飞，男，1996年生，硕士研究生。主要研究方向：金刚石刀具的超精密加工制造。E-mail：190595501@qq.com

中图分类号: TG58；TQ164
计量
- 文章访问数: 909
- HTML全文浏览量: 314
- PDF下载量: 93
- 被引次数: 0
出版历程
- 收稿日期: 2022-04-14
- 修回日期: 2022-07-11
- 录用日期: 2022-07-13
- 刊出日期: 2023-02-20

Diamond grinding quality analysis based on controlled grinding depth

PANG Fei^{1, 2
,},
LEI Dajiang¹,
WANG Wei²

1.
Institute of Machinery Manufacturing Technology, China Academy of Engineering Physics, Mianyang 621000, Sichuan, China
2.
School of Mechanical and Electrical Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China

摘要

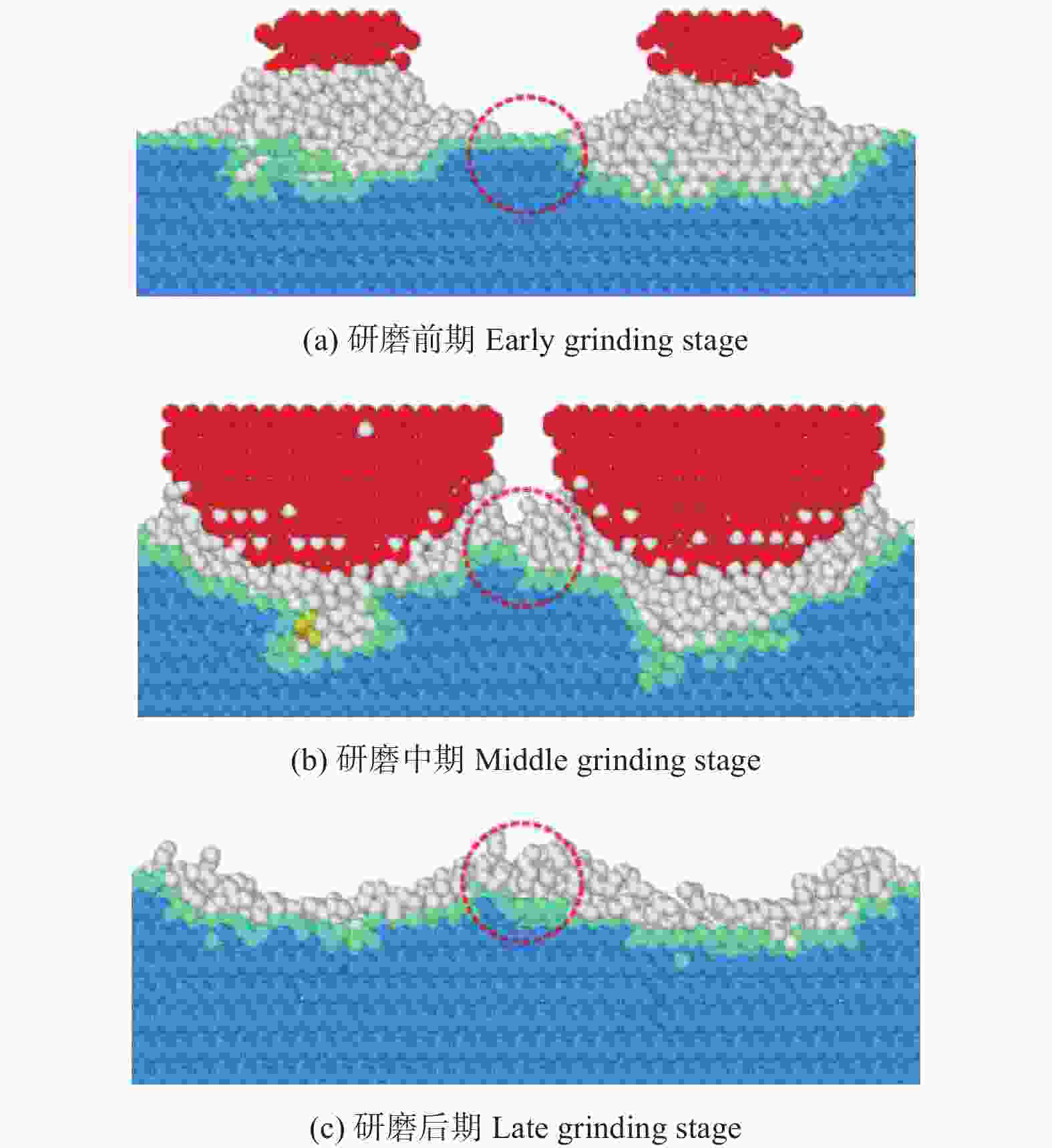
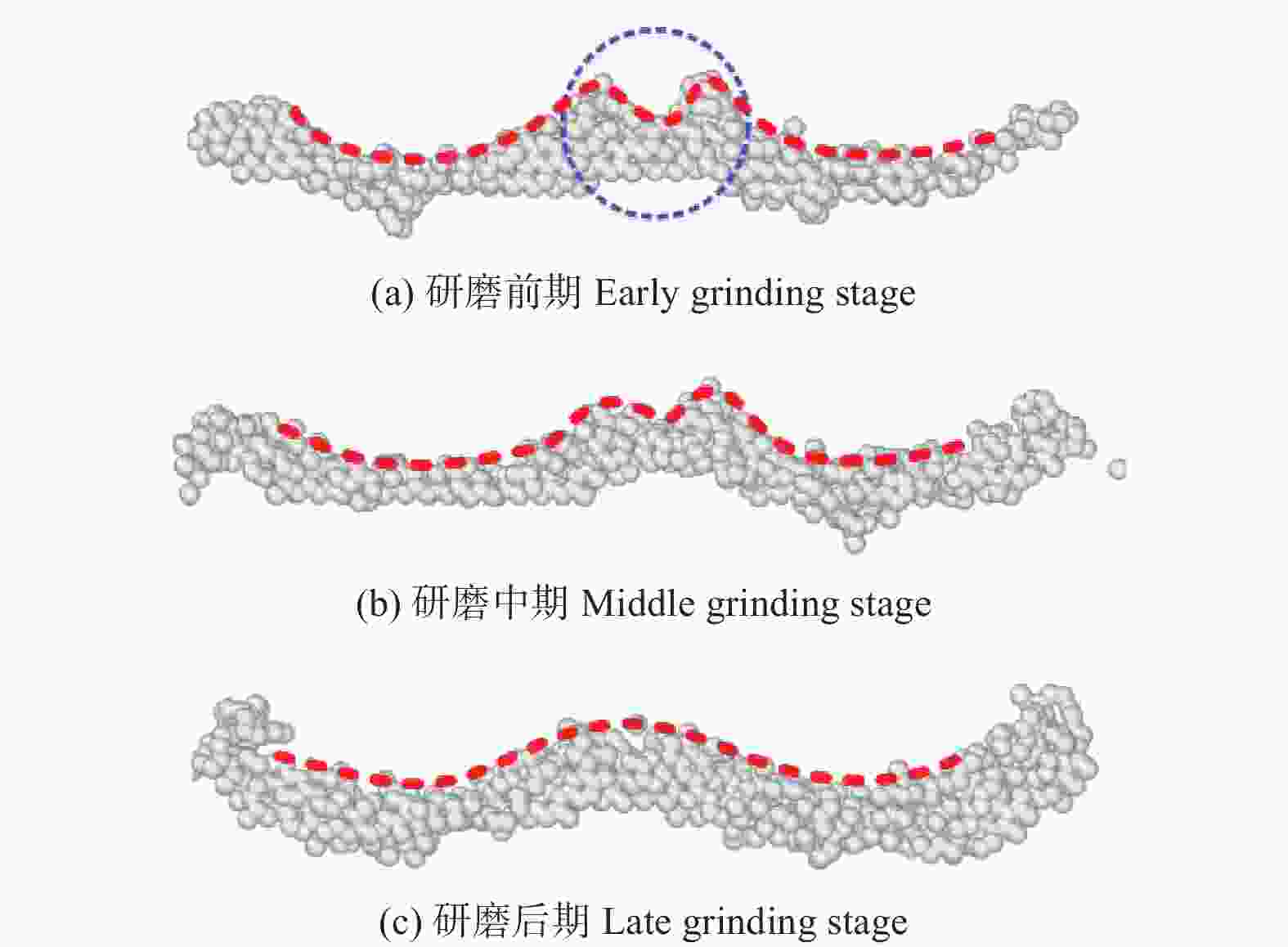
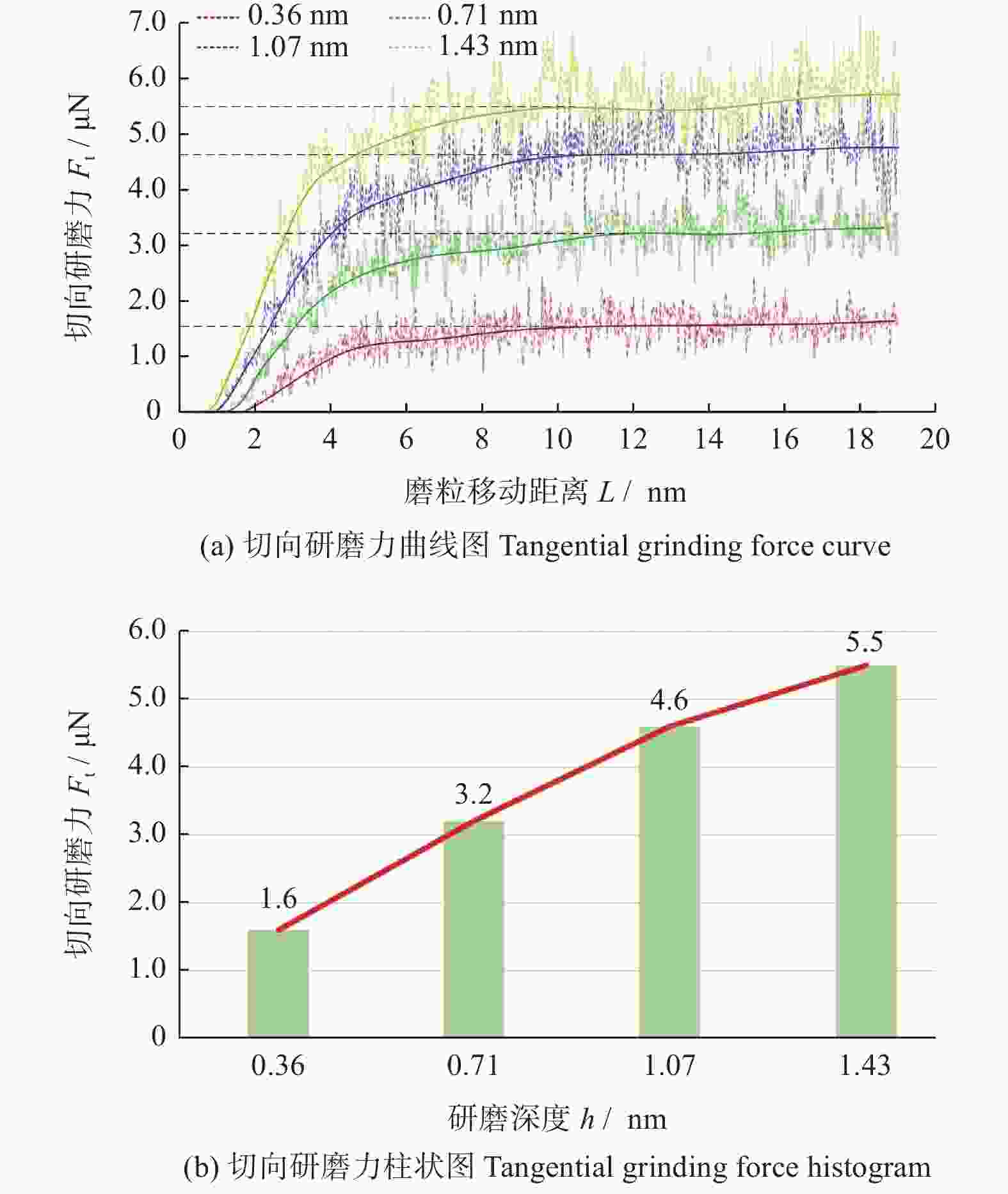
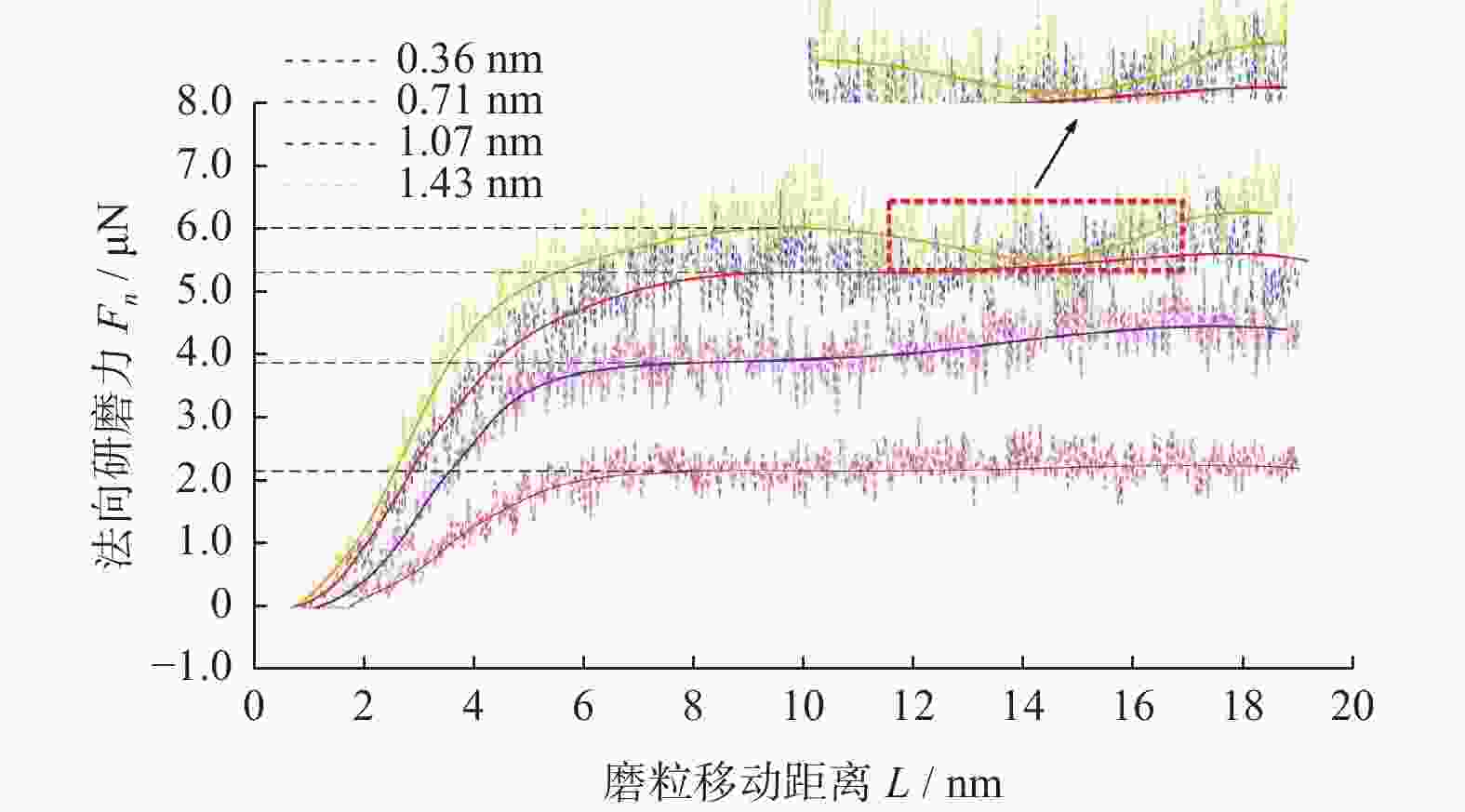
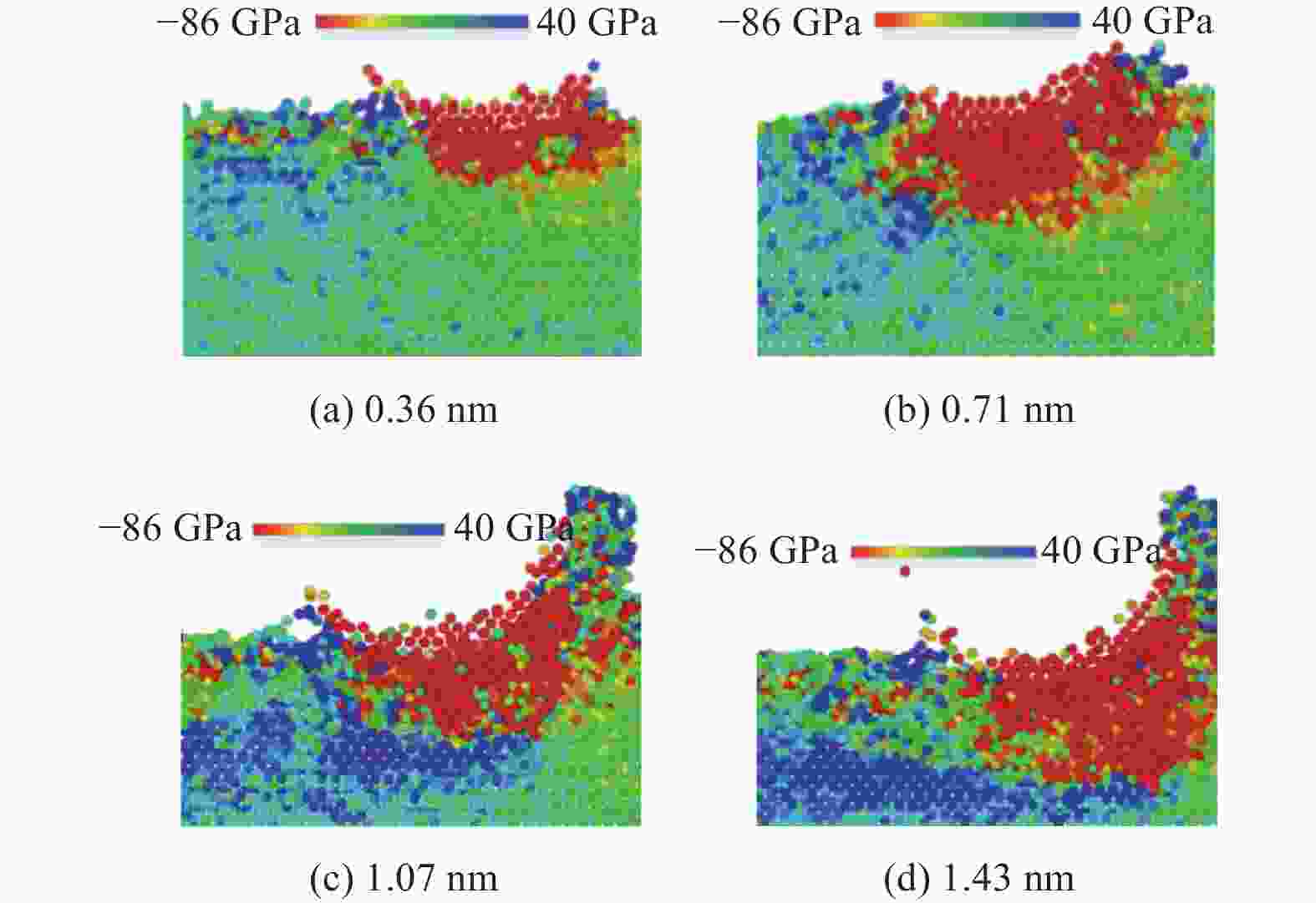
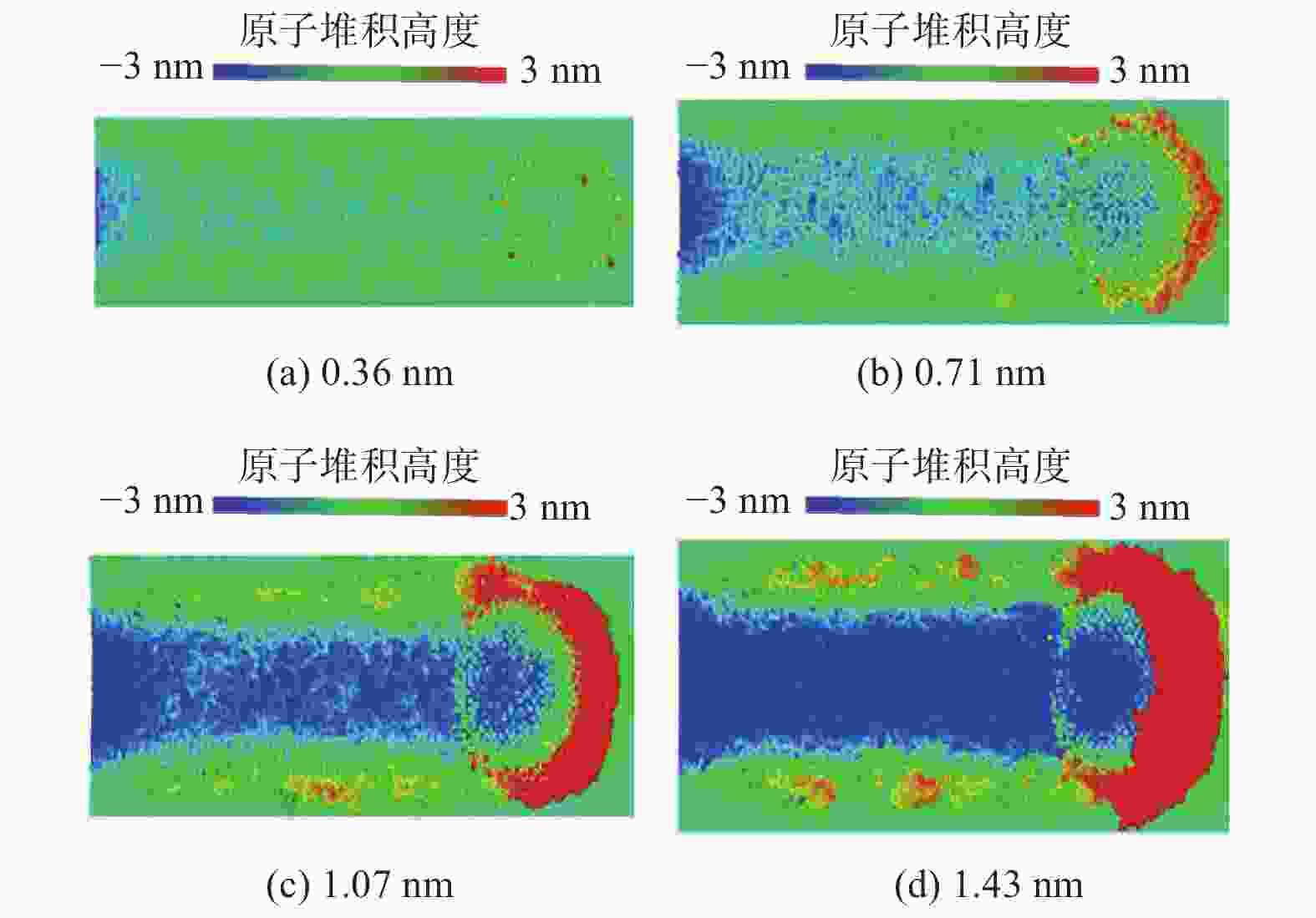
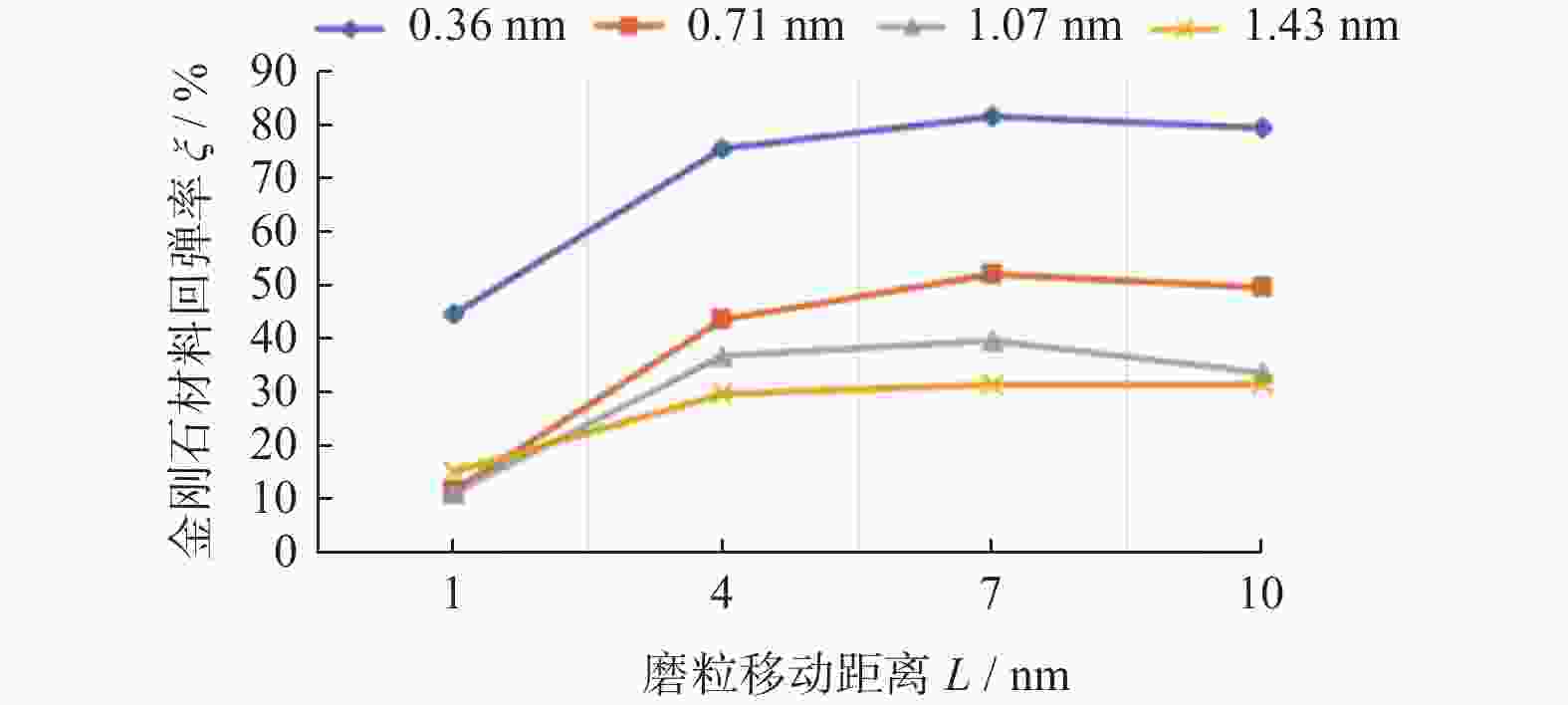
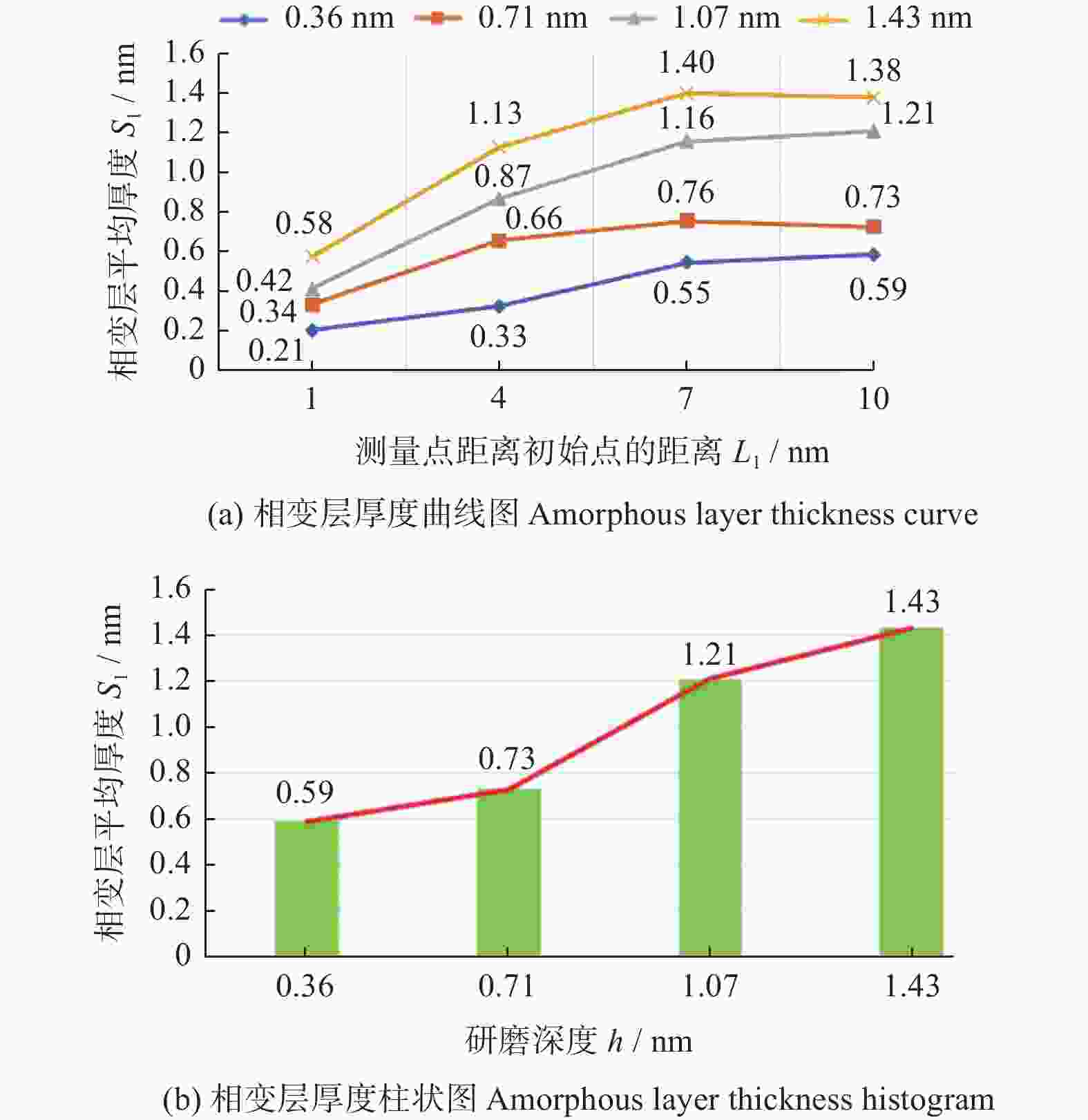
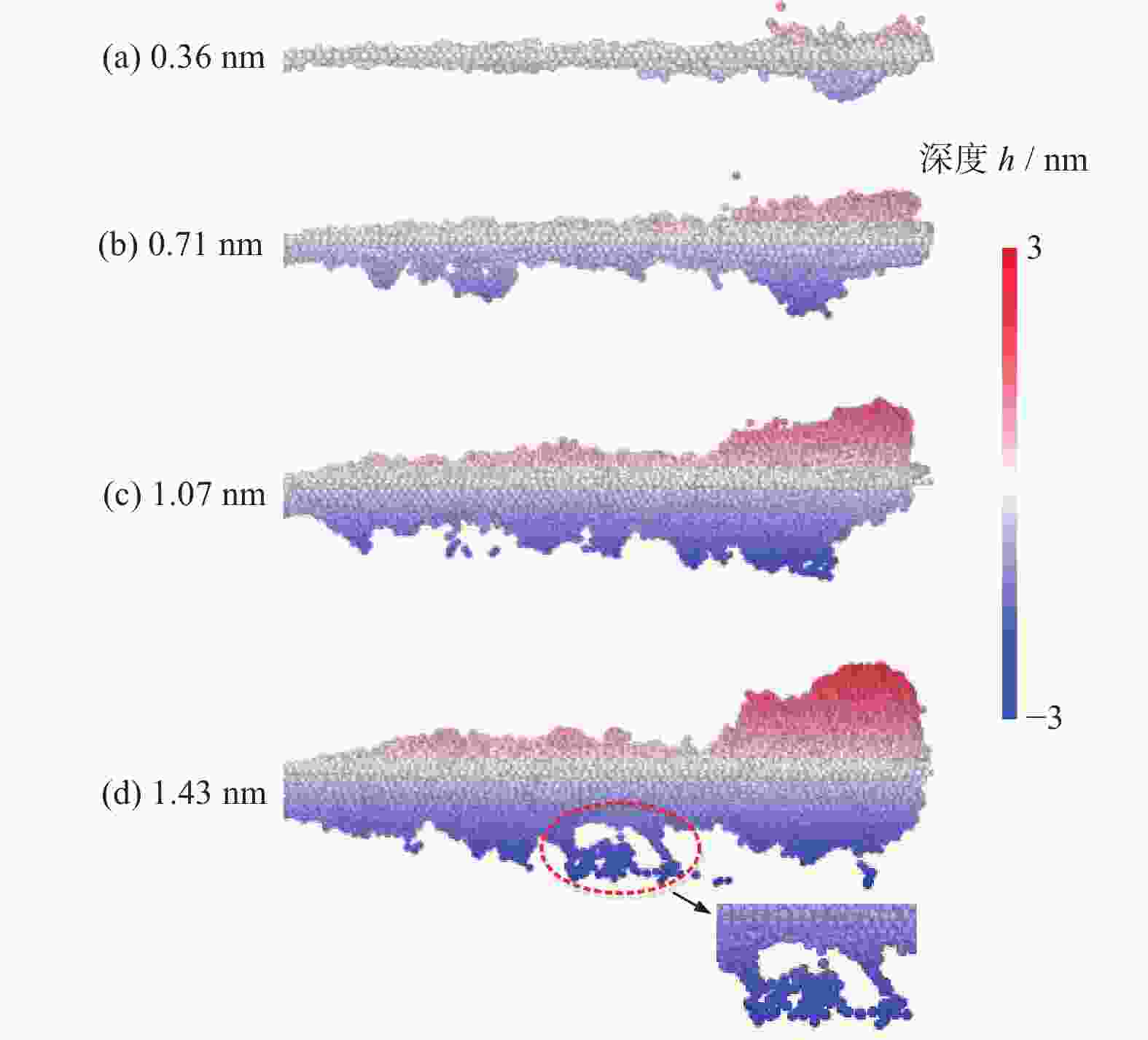
摘要: 为了探究金刚石器件在机械研磨过程中原子层面的材料表面成形和亚表面损伤机制，利用分子动力学（molecular dynamics，MD）方法建立金刚石多磨粒研磨金刚石工件的模型，仿真研究金刚石材料表面成形的过程，并对比不同研磨深度对研磨力、材料回弹率和材料亚表面损伤的影响规律。分析表明：堆积在磨粒之间的切屑原子具有微研磨的作用，磨粒之间的相变区在研磨的作用下逐渐融合在一起，形成金刚石材料的加工表面；分别以h=0.36 nm、0.71 nm、1.07 nm、1.43 nm的研磨深度进行研磨，研磨深度超过0.71 nm后才能有效抑制金刚石晶体材料回弹，但增大研磨深度会增加金刚石工件表面堆积原子，不能改善其表面研磨质量；研磨深度在0.71 nm范围内的金刚石亚表层损伤较小且稳定，超过0.71 nm的研磨深度会使损伤快速增大，且会出现超过3.00 nm的大纵深损伤。
- 分子动力学 /
- 金刚石 /
- 研磨深度 /
- 亚表面损伤
Abstract: In order to explore the surface grinding quality and subsurface damage law of the grinding depth on the diamond material, the model of diamond workpiece ground by multi grits is established by molecular dynamics (MD) method. The effect of different grinding depths on the grinding force, the grinding quality of the surface and the subsurface damage characteristics of the material is studied. The analysis shows that the chip atoms accumulated between the grits have the effect of micro-grinding, and that the amorphous area between the grits is gradually fused together under the action of grinding to form the processing surface of the diamond material. The grinding depths of h = 0.36 nm, 0.71 nm, 1.07 nm and 1.43 nm are used respectively. The springback of diamond crystal material can be effectively inhibited only when the grinding depth exceeds 0.71 nm. However, increasing the grinding depth will increase the accumulation of atoms on the surface of diamond workpiece, which cannot improve the grinding quality. At the same time, the increase of the grinding depth will intensify the subsurface damage to the diamond workpiece. The subsurface damage of the material with a grinding depth below 0.71 nm is small and stable. However, the damage increases rapidly when the grinding depth exceeds 0.71 nm and large-depth damage over 3 nm appears on the subsurface.
- molecular dynamics /
- diamond /
- grinding depth /
- subsurface damage

HTML全文

图 1 磨粒研磨的分子动力学模型

Figure 1. MD model of abrasive grinding

下载: 全尺寸图片幻灯片

图 2 磨粒研磨作用下金刚石工件原子的相变

Figure 2. Atomic amorphization of diamond workpiece in abrasive grinding

下载: 全尺寸图片幻灯片

图 3 研磨造成的相变层变化

Figure 3. Change of amorphous layer caused by grinding

下载: 全尺寸图片幻灯片

图 4 磨粒研磨模型示意图

Figure 4. Schematic diagram of abrasive grinding model

下载: 全尺寸图片幻灯片

图 5 不同研磨深度下磨粒的切向研磨力变化

Figure 5. Tangential grinding force variation of abrasives at different grinding depths

下载: 全尺寸图片幻灯片

图 6 不同研磨深度下磨粒的法向研磨力变化

Figure 6. Normal grinding force variation of abrasives at different grinding depths

下载: 全尺寸图片幻灯片

图 7 不同研磨深度下的原子堆积

Figure 7. Atomic build-up at different grinding depths

下载: 全尺寸图片幻灯片

图 8 不同研磨深度下工件切片的应力分布

Figure 8. Stress distribution of workpiece sections at different grinding depths

下载: 全尺寸图片幻灯片

图 9 不同研磨深度下工件表面形貌

Figure 9. Surface morphology of the workpiece at different grinding depths

下载: 全尺寸图片幻灯片

图 10 金刚石工件的材料回弹现象

Figure 10. Material rebound phenomenon of diamond workpieces

下载: 全尺寸图片幻灯片

图 11 不同研磨深度下金刚石材料回弹率变化

Figure 11. Rebound rate of diamond material changes at different grinding depths

下载: 全尺寸图片幻灯片

图 12 工件亚表面损伤厚度测量示意图

Figure 12. Schematic diagram of workpiece subsurface damage thickness measurement

下载: 全尺寸图片幻灯片

图 13 不同研磨深度下的工件相变层平均厚度变化曲线

Figure 13. Change curve of amorphous layer thickness of workpiece under different grinding depth

下载: 全尺寸图片幻灯片

图 14 不同研磨深度下的金刚石工件的原子相变

Figure 14. Atomic phase transition diagram of diamond workpiece at different grinding depths

下载: 全尺寸图片幻灯片

图 15 金刚石研磨系统局部图

Figure 15. Local diagram of the diamond grinding system

下载: 全尺寸图片幻灯片

图 16 测量简图

Figure 16. Measurement sketch

下载: 全尺寸图片幻灯片

图 17 不同压力研磨下的表面形貌

Figure 17. Surface morphology under different pressures

下载: 全尺寸图片幻灯片

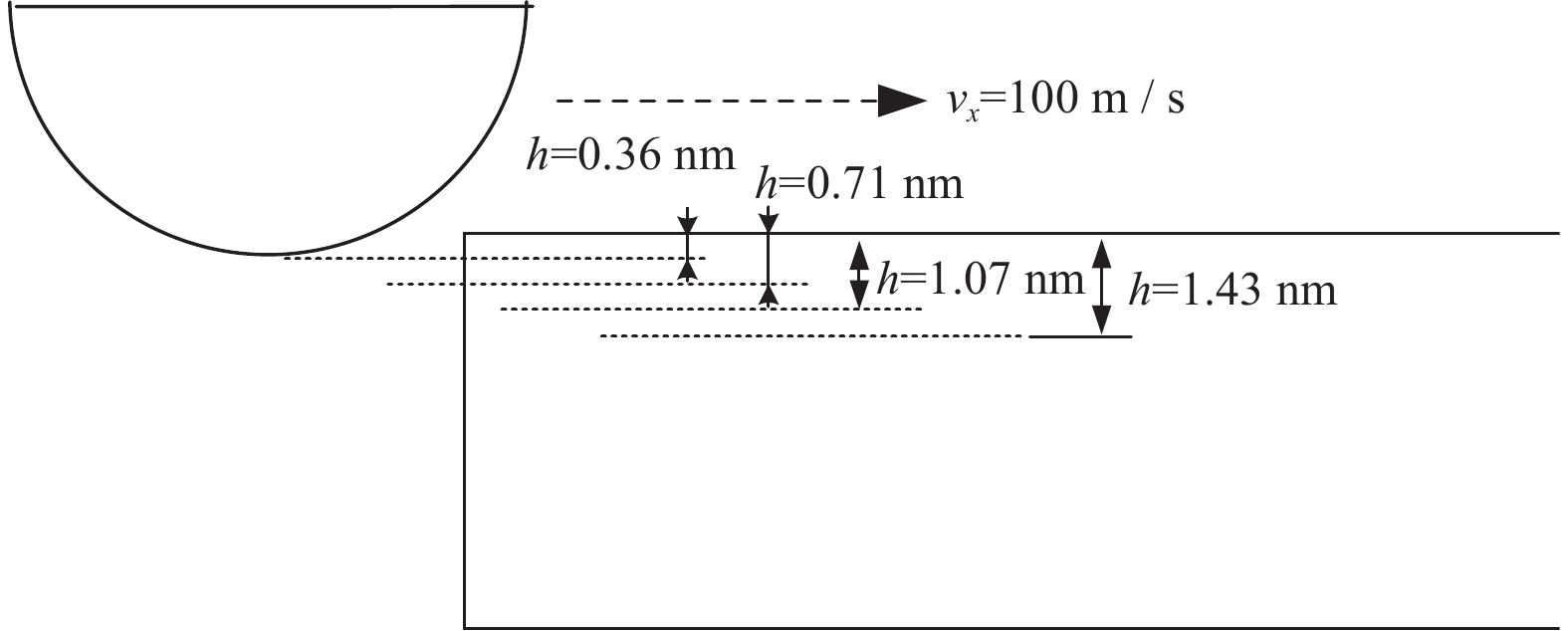
表 1 分子动力学仿真试验参数

Table 1. MD simulation test parameters

参数	条件或取值
刻划晶面	（0 0 1）
刻划方向	[1 0 0]
刻划速度 $ {v_x} $ / (m·s⁻¹)	100
研磨深度 h / nm	0.36, 0.71, 1.07, 1.43
磨粒移动距离 L / nm	18.5
时间步长 t / fs	0.5

下载: 导出CSV

表 2 模型具体参数设置^[14]

Table 2. Model specific parameter settings^[14]

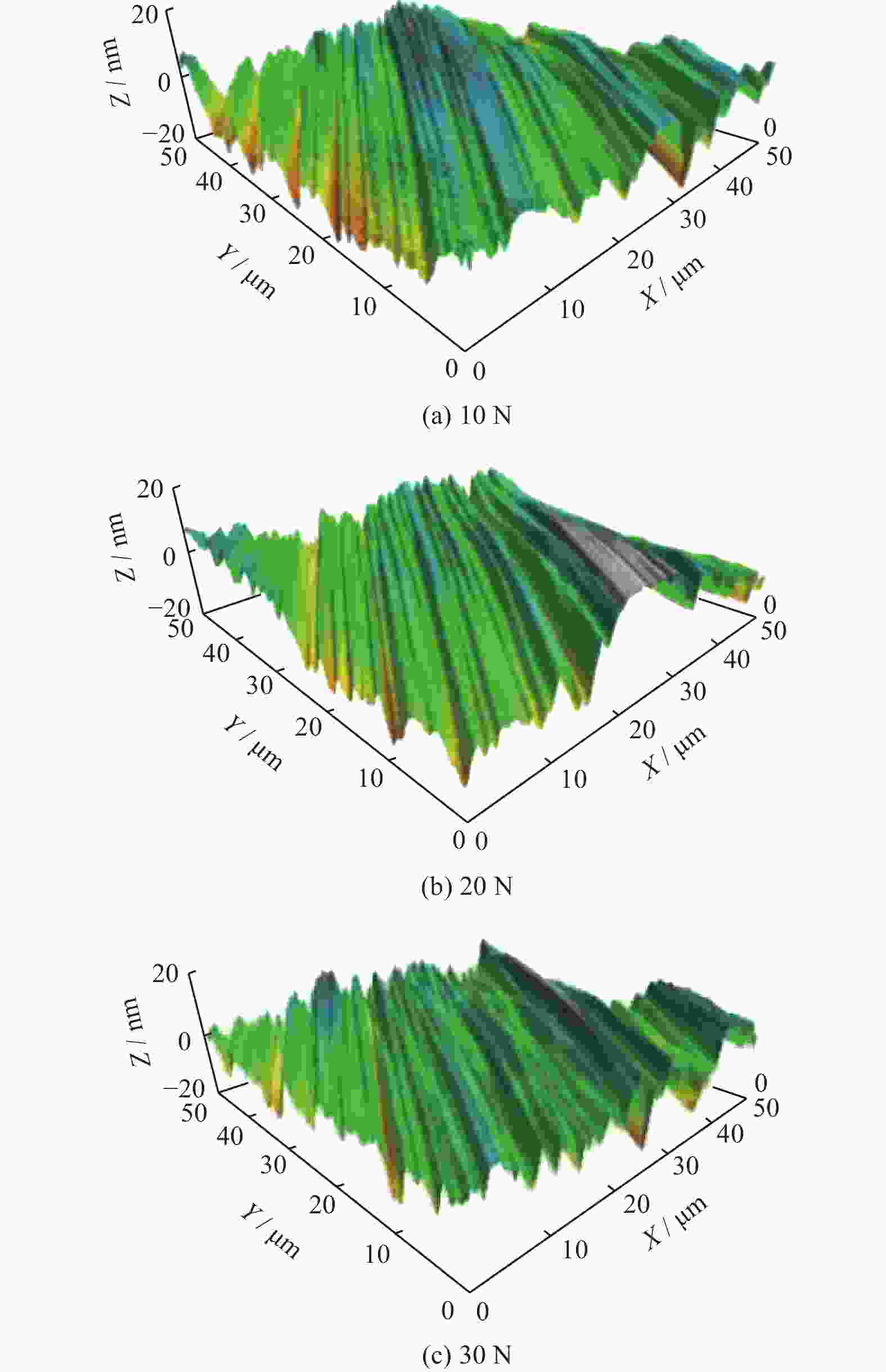
吸引项结合能 $ A $ / eV	排斥项结合能 $ B $ / eV	吸引项势能梯度系数 $ \lambda $ / (nm⁻¹)	排斥项势能梯度系数 $ \mu $ / (nm⁻¹)	键级函数值 $ \beta $	调制函数系数 $ n $	键角函数系数 $ c $	键角函数系数 $ d $	键角函数系数 $ h $	第一截断距离 $ R $ / nm	第二截断距离$ S $ / nm
1 393.6	346.7	34.88	22.12	1.57×10⁻⁷	0.73	38 049	4.35	−0.57	0.195	0.21

下载: 导出CSV

表 3 工件表面粗糙度测量结果

Table 3. Measurement results of the surface roughness of the workpiece

研磨压力 F / N	表面粗糙度值 R_a/ nm
10	3.259
20	5.696
30	8.015

下载: 导出CSV

参考文献(14)

[1]	高凯, 李志宏. 金刚石材料的功能特性研究与应用 [J]. 真空电子技术,2010(4):9-13. doi: 10.3969/j.issn.1002-8935.2010.04.003 GAO Kai, LI Zhihong. Research and application of functional properties of diamond materials [J]. Vacuum Electronics,2010(4):9-13. doi: 10.3969/j.issn.1002-8935.2010.04.003
[2]	宗文俊, 孙涛, 李旦, 等. 单晶金刚石晶体的机械研磨 [J]. 哈尔滨工业大学学报,2005(8):1036-1038,1045. doi: 10.3321/j.issn:0367-6234.2005.08.006 ZONG Wenjun, SUN Tao, LI Dan, et al. Mechanical grinding of monocrystal diamond [J]. Journal of Harbin Institute of Technology,2005(8):1036-1038,1045. doi: 10.3321/j.issn:0367-6234.2005.08.006
[3]	张桐齐, 岳晓斌, 雷大江, 等. 磨粒半径对金刚石研磨加工影响机制的仿真研究 [J]. 金刚石与磨料磨具工程,2021,41(1):89-94. doi: 10.13394/j.cnki.jgszz.2021.1.0015 ZHANG Tongqi, YUE Xiaobin, LEI Dajiang, et al. Simulation study on the influence mechanism of abrasive radius on diamond grinding [J]. Diamond & Abrasives Engineering,2021,41(1):89-94. doi: 10.13394/j.cnki.jgszz.2021.1.0015
[4]	张斌, 董荣娟. 纳米金刚石中(I/Ⅱ)复合裂纹的分子动力学研究 [J]. 机械强度,2012(5):672-676. ZHANG Bin, DONG Rongjuan. Molecular dynamics study of (I/Ⅱ) composite cracks in nano-diamond [J]. Journal of Mechanical Strength,2012(5):672-676.
[5]	李增强, 宗文俊, 孙涛, 等. 金刚石刀具机械研磨过程中材料的去除机理 [J]. 纳米技术与精密工程,2009,7(1):31-35. doi: 10.3969/j.issn.1672-6030.2009.01.007 LI Zengqiang, ZONG Wenjun, SUN Tao, et al. Mechanism of material removal during mechanical grinding of diamond tools [J]. Nanotechnology and Precision Engineering,2009,7(1):31-35. doi: 10.3969/j.issn.1672-6030.2009.01.007
[6]	LI X W, WANG A Y, LEE K R. Insights on low-friction mechanism of amorphous carbon films from reactive molecular dynamics study [J]. Tribology International,2019,131:567-578. doi: 10.1016/j.triboint.2018.11.021
[7]	EDER S J, CIHAK-BAYER U, PAUSCHITZ A. Nanotribological simulations of multi-grit polishing and grinding [J]. Wear,2015:340-341.
[8]	郭晓光, 张亮, 金洙吉, 等. 分子动力学仿真过程中硅晶体位错模型的构建 [J]. 中国机械工程,2013,24(17):2285-2289. doi: 10.3969/j.issn.1004-132X.2013.17.003 GUO Xiaoguang, ZHANG Liang, JIN Zhuji, et al. Construction of dislocation model of silicon crystal in molecular dynamics simulation [J]. China Mechanical Engineering,2013,24(17):2285-2289. doi: 10.3969/j.issn.1004-132X.2013.17.003
[9]	LIU C L, HE W B, CHU J N, et al. Molecular dynamics simulation on cutting mechanism in the hybrid machining process of single-crystal silicon [J]. Nanoscale Research Letters, 2021, 16(1): 66.
[10]	YANG N, ZONG W J, LI Z Q, et al. Amorphization anisotropy and the internal of amorphous layer in diamond nanoscale friction [J]. Computational Materials Science,2014,95:551-556. doi: 10.1016/j.commatsci.2014.08.040
[11]	YANG N, XIA Z H, WANG X J. Phase change of carbon atoms in surface layer under nanocutting during diamond lapping process [J]. Journal of Tribology,2018,71:140-143.
[12]	杨宁. 高精度天然金刚石刀具可控刃磨的若干问题研究 [D]. 哈尔滨: 哈尔滨工业大学, 2015. YANG Ning. Research on some problems for controllable lapping of high precision natural diamond cutting tool [D]. Harbin: Harbin Institute of Technology, 2015.
[13]	程晓. 天然金刚石刀具机械研磨机理与微铣刀制造关键技术研究 [D]. 哈尔滨: 哈尔滨工业大学, 2020. CHENG Xiao. Research on mechanism of mechnical lapping of natural diamond tools and key technology of manufacturing micro milling tools [D]. Harbin: Harbin Institute of Technology, 2020.
[14]	TERSOFF J. Empirical interatomic potential for carbon, with application to amorphous carbon [J]. Physical Review Letters,1988,61(25):2879-2882. doi: 10.1103/PhysRevLett.61.2879